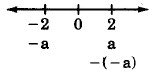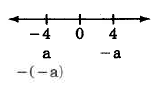1. Home
  2. Algebra i for the community
  3. Chapter 1: introduction to real
  4. Chapter 1 part a
  5. Real numbers

Real numbers

<< Chapter < Page
  Algebra i for the community   Page 1 / 1
Chapter >> Page >
This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses signed numbers. By the end of the module students be able to distinguish between positive and negative real numbers, be able to read signed numbers and understand the origin and use of the double-negative product property.

Section overview

  • Positive and Negative Numbers
  • Reading Signed Numbers
  • Opposites
  • The Double-Negative Property

Positive and negative numbers

Positive and negative numbers

Each real number other than zero has a sign associated with it. A real number is said to be a positive number if it is to the right of 0 on the number line and negative if it is to the left of 0 on the number line.

The notation of signed numbers

+ and - Notation

A number is denoted as positive if it is directly preceded by a plus sign or no sign at all.
A number is denoted as negative if it is directly preceded by a minus sign.

Reading signed numbers

The plus and minus signs now have two meanings :

The plus sign can denote the operation of addition or a positive number.

The minus sign can denote the operation of subtraction or a negative number.

To avoid any confusion between "sign" and "operation," it is preferable to read the sign of a number as "positive" or "negative." When "+" is used as an operation sign, it is read as "plus." When " - " is used as an operation sign, it is read as "minus."

Sample set a

Read each expression so as to avoid confusion between "operation" and "sign."

- 8 should be read as "negative eight" rather than "minus eight."

4 + ( - 2 ) size 12{"4 "+ \( "–2" \) } {} should be read as "four plus negative two" rather than "four plus minus two."

- 6 + ( - 3 ) size 12{"–6 "+ \( "–3" \) } {} should be read as "negative six plus negative three" rather than "minus six plus minus three."

- 15 - ( - 6 ) size 12{"–15 – " \( "–6" \) } {} should be read as "negative fifteen minus negative six" rather than "minus fifteen minus minus six."

- 5 + 7 size 12{"–5 "+" 7"} {} should be read as "negative five plus seven" rather than "minus five plus seven."

0 - 2 size 12{"0 – 2"} {} should be read as "zero minus two."

Practice set a

Write each expression in words.

6 + 1 size 12{"6 "+" 1"} {}

six plus one

2 + ( - 8 ) size 12{2+ \( "–8" \) } {}

two plus negative eight

- 7 + 5 size 12{"–7"+5} {}

negative seven plus five

- 10 - ( + 3 ) size 12{"–10 – " \( +3 \) } {}

negative ten minus three

- 1 - ( - 8 ) size 12{"–1 –" \( "–8" \) } {}

negative one minus negative eight

0 + ( - 11 ) size 12{"0 "+ \( "–11" \) } {}

zero plus negative eleven

Opposites

Opposites

On the number line, each real number, other than zero, has an image on the opposite side of 0. For this reason, we say that each real number has an opposite. Opposites are the same distance from zero but have opposite signs.

The opposite of a real number is denoted by placing a negative sign directly in front of the number. Thus, if a size 12{a} {} is any real number, then − a size 12{ - a} {} is its opposite.

The letter " a size 12{a} {} " is a variable. Thus, " a size 12{a} {} " need not be positive, and " - a size 12{–a} {} " need not be negative.

If a size 12{a} {} is any real number, − a size 12{ - a} {} is opposite a size 12{a} {} on the number line.

Two number lines. One number line with hash marks from left to right, -a, 0, and a. This number line is titled a positive. A second number line with hash marks from left to right, a, 0, and -a. This number line is titled a negative.

The double-negative property

The number a size 12{a} {} is opposite − a size 12{ - a} {} on the number line. Therefore, − ( − a ) size 12{ - \( - a \) } {} is opposite − a size 12{ - a} {} on the number line. This means that

− ( − a ) = a size 12{ - \( - a \) =a} {}

From this property of opposites, we can suggest the double-negative property for real numbers.

Double-negative property: − ( − a ) = a size 12{ - \( - a \) =a} {}

If a size 12{a} {} is a real number, then
− ( − a ) = a size 12{ - \( - a \) =a} {}

Sample set b

Find the opposite of each number.

If a = 2 size 12{"a "=" 2"} {} , then - a = - 2 size 12{"–a "=" –2"} {} . Also, − ( − a ) = − ( − 2 ) = 2 size 12{ - \( - a \) = - \( - 2 \) =2} {} .

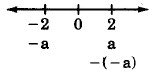
A number line with hash marks from left to right, -2, 0, and 2. Below the -2 is -a, and below the 2 is a, or -(-a).

If a = - 4 size 12{"a "=" –4"} {} , then - a = - ( - 4 ) = 4 size 12{"–a "="– " \( "–4" \) =" 4"} {} . Also, - ( - a ) = a = - 4 size 12{– \( "–a" \) =" a "= – " 4"} {} .

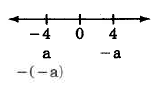
A number line with hash marks from left to right, -4, 0, and 4. Below the -4 is a, or -(-a), and below the 2 is -a.

Practice set b

Find the opposite of each number.

8

-8

17

-17

-6

6

-15

15

-(-1)

-1

- [ - ( - 7 ) ]

7

Suppose a size 12{a} {} is a positive number. Is − a size 12{ - a} {} positive or negative?

− a size 12{ - a} {} is negative

Suppose a size 12{a} {} is a negative number. Is − a size 12{ - a} {} positive or negative?

− a size 12{ - a} {} is positive

Suppose we do not know the sign of the number k size 12{k} {} . Is − k size 12{ - k} {} positive, negative, or do we not know?

We must say that we do not know.

Exercises

A number is denoted as positive if it is directly preceded by .

+ (or no sign)

A number is denoted as negative if it is directly preceded by .

How should the number in the following 6 problems be read? (Write in words.)

− 7 size 12{-7} {}

negative seven

− 5 size 12{-5} {}

15 size 12{"15"} {}

fifteen

11

− − 1 size 12{- left (-1 right )} {}

negative negative one, or opposite negative one

− − 5 size 12{- left (-5 right )} {}

For the following 6 problems, write each expression in words.

5 + 3 size 12{5+3} {}

five plus three

3 + 8 size 12{3+8} {}

15 + − 3 size 12{"15"+ left (-3 right )} {}

fifteen plus negative three

1 + − 9 size 12{1+ left (-9 right )} {}

− 7 − − 2 size 12{-7- left (-2 right )} {}

negative seven minus negative two

0 − − 12 size 12{0- left (-"12" right )} {}

For the following 6 problems, rewrite each number in simpler form.

− − 2 size 12{- left (-2 right )} {}

2

− − 16 size 12{- left (-"16" right )} {}

− − − 8 size 12{- left [- left (-8 right ) right ]} {}

-8

− − − 20 size 12{- left [- left (-"20" right ) right ]} {}

7 − − 3 size 12{7- left (-3 right )} {}

7 + 3 = 10 size 12{7+3="10"} {}

6 − − 4 size 12{6- left (-4 right )} {}

Exercises for review

( [link] ) Find the quotient; 8 ÷ 27 size 12{8÷"27"} {} .

0 . 296 ¯ size 12{0 "." {overline {"296"}} } {}

( [link] ) Solve the proportion: 5 9 = 60 x size 12{ { {5} over {9} } = { {"60"} over {x} } } {}

( [link] ) Use the method of rounding to estimate the sum: 5829 + 8767 size 12{"5829"+"8767"} {}

6, 000 + 9, 000 = 15 , 000   ( 5, 829 + 8, 767 = 14 , 59 6 )   or 5, 800 + 8, 800 = 14 , 600 size 12{6,"000"+9,"000"="15","000" \( 5,"829"+8,"767"="14","59"6 \) " or 5,""800"+8,"800"="14","600"} {}

( [link] ) Use a unit fraction to convert 4 yd to feet.

( [link] ) Convert 25 cm to hm.

0.0025 hm
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Algebra i for the community college. OpenStax CNX. Dec 19, 2014 Download for free at http://legacy.cnx.org/content/col11598/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra i for the community college' conversation and receive update notifications?

Ask