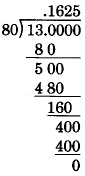1.6 Decimal fractions

Basic mathematics review Page 1 / 1

This module is from Elementary Algebra by Denny Burzynski and Wade Ellis, Jr. This chapter contains many examples of arithmetic techniques that are used directly or indirectly in algebra. Since the chapter is intended as a review, the problem-solving techniques are presented without being developed. Therefore, no work space is provided, nor does the chapter contain all of the pedagogical features of the text. As a review, this chapter can be assigned at the discretion of the instructor and can also be a valuable reference tool for the student.

Overview

Decimal Fractions
Adding and Subtracting Decimal Fractions
Multiplying Decimal Fractions
Dividing Decimal Fractions
Converting Decimal Fractions to Fractions
Converting Fractions to Decimal Fractions

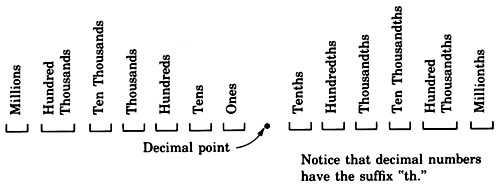
Decimal fractions

Fractions are one way we can represent parts of whole numbers. Decimal fractions are another way of representing parts of whole numbers.

Decimal fractions

A decimal fraction is a fraction in which the denominator is a power of 10.

A decimal fraction uses a decimal point to separate whole parts and fractional parts. Whole parts are written to the left of the decimal point and fractional parts are written to the right of the decimal point. Just as each digit in a whole number has a particular value, so do the digits in decimal positions.

Sample set a

The following numbers are decimal fractions.

$\begin{array}{l} 57.9 \\ The 9 is in the t e n t h s position . 57.9 = 57 \frac{9}{10} . \end{array}$

$\begin{array}{l} 6.8014 \\ The 8 is in the t e n t h s position . \\ The 0 is in the h u n d r e d t h s position . \\ The 1 is in the t h o u s a n d t h s position . \\ The 4 is in the ten t h o u s a n d t h s position . \\ 6.8014 = 6 \frac{8014}{10000} . \end{array}$

Adding and subtracting decimal fractions

Adding/subtracting decimal fractions

To add or subtract decimal fractions,

Align the numbers vertically so that the decimal points line up under each other and corresponding decimal positions are in the same column. Add zeros if necessary.
Add or subtract the numbers as if they were whole numbers.
Place a decimal point in the resulting sum or difference directly under the other decimal points.

Sample set b

Find each sum or difference.

$\begin{array}{l} 9.183 + 2.140 \\ \begin{array}{r} ↓ & The decimal points are aligned in the same column . \\ 9 .183 \\ + \underline{2 .140} \\ 11 .323 \end{array} \end{array}$

$\begin{array}{l} 841.0056 + 47.016 + 19.058 \\ \begin{array}{r} ↓ & The decimal points are aligned in the same column . \\ 841.0056 \\ 47.016 & Place a 0 into the thousandths position . \\ + \underline{19.058} & Place a 0 into the thousandths position . \\ ↓ & The decimal points are aligned in the same column . \\ 841.0056 \\ 47.0160 \\ + \underline{19.0580} \\ 907.0796 \end{array} \end{array}$

$\begin{array}{l} 16.01 - 7.053 \\ \begin{array}{r} ↓ & The decimal points are aligned in the same column . \\ 16.01 & Place a 0 into the thousandths position . \\ - \underline{7.053} \\ ↓ & The decimal points are aligned in the same column . \\ 16.010 \\ - \underline{7.053} \\ 8.957 \end{array} \end{array}$

Multiplying decimal fractions

To multiply decimals,

Multiply tbe numbers as if they were whole numbers.
Find the sum of the number of decimal places in the factors.
The number of decimal places in the product is the sum found in step 2.

Sample set c

Find the following products.

$6.5 \times 4.3$

The vertical multiplication of two decimals; six point five, and four point three. See the longdesc for a full description.

$6.5 \times 4.3 = 27.95$

$23.4 \times 1.96$

The vertical multiplication of two decimals; twenty-three point four, and one point nine six. See the longdesc for a full description.

$23.4 \times 1.96 = 45.864$

Dividing decimal fractions

To divide a decimal by a nonzero decimal,

Convert the divisor to a whole number by moving the decimal point to the position immediately to the right of the divisor’s last digit.
Move the decimal point of the dividend to the right the same number of digits it was moved in the divisor.
Set the decimal point in the quotient by placing a decimal point directly above the decimal point in the dividend.
Divide as usual.

Sample set d

Find the following quotients.

$32.66 \div 7.1$

A long division problem showing seven point one dividing thirty-two point six six. See the longdesc for a full description.

$\begin{array}{l} 32.66 \div 7.1 = 4.6 \\ \begin{array}{l} C h e c k : & 32.66 \div 7.1 = 4.6 if 4.6 \times 7.1 = 32.66 \\ 4.6 \\ \underline{7.1} \\ 4.6 \\ \underline{322} \\ 32.66 & True \end{array} \end{array}$

A long division problem showing zero point five one three dividing one point zero seven seven three. See the longdesc for a full description.

Check by multiplying $2.1$ and $0.513.$ This will show that we have obtained the correct result.

$12 \div 0.00032$ A long division problem showing zero point zero zero zero three two dividing twelve. See the longdesc for a full description.

Converting decimal fractions to fractions

We can convert a decimal fraction to a fraction by reading it and then writing the phrase we have just read. As we read the decimal fraction, we note the place value farthest to the right. We may have to reduce the fraction.

Sample set e

Convert each decimal fraction to a fraction.

$\begin{array}{l} 0.6 \\ 0. \underline{6} \to tenths position \\ \begin{array}{l} Reading: & six tenths \to \frac{6}{10} \\ Reduce: & 0.6 = \frac{6}{10} = \frac{3}{5} \end{array} \end{array}$

$\begin{array}{l} 21.903 \\ 21.90 \underline{3} \to thousandths position \\ \begin{matrix} Reading: & twenty-one and nine hundred three thousandths \to 21 \frac{903}{1000} \end{matrix} \end{array}$

Converting fractions to decimal fractions

Sample set f

Convert the following fractions to decimals. If the division is nonterminating, round to 2 decimal places.

$\frac{3}{4}$

A long division problem showing four dividing three point zero zero. See the longdesc for a full description.

$\frac{3}{4} = 0.75$

$\frac{1}{5}$

A long division problem showing five dividing one point zero. The quotient is point two. The result of point two, multiplied by the divisor, five, is one point zero written under the dividend one point zero. The remainder zero is written as a result of the subtraction of one point zero and one point zero. A comment 'Divide one by five' is written on the right side of the problem.

$\frac{1}{5} = 0.2$

$\frac{5}{6}$

A long division problem showing six dividing five point zero zero zero. See the longdesc for a full description.

$\begin{array}{l} \frac{5}{6} & = & 0.833... & \begin{array}{l} We are to round to 2 decimal places . \end{array} \\ \frac{5}{6} & = & 0.83 to 2 decimal places . \end{array}$

$\begin{array}{l} 5 \frac{1}{8} \\ Note that 5 \frac{1}{8} = 5 + \frac{1}{8} . \end{array}$

One point zero zero zero is being divided by eight, using long division method. See the longdesc for a full description.

$\begin{array}{l} \frac{1}{8} = .125 \\ Thus, 5 \frac{1}{8} = 5 + \frac{1}{8} = 5 + .125 = 5.125. \end{array}$

$0.16 \frac{1}{4}$

This is a complex decimal. The “6” is in the hundredths position. The number $0.16 \frac{1}{4}$ is read as “sixteen and one-fourth hundredths.”

$\begin{array}{l} 0.16 \frac{1}{4} = \frac{16 \frac{1}{4}}{100} = \frac{\frac{16 \cdot 4 + 1}{4}}{100} & = & \frac{\frac{65}{4}}{\frac{100}{1}} \\ = & \frac{\overset{13}{65}}{4} \cdot \frac{1}{\underset{20}{100}} = \frac{13 \times 1}{4 \times 20} = \frac{13}{80} \end{array}$

Now, convert $\frac{13}{80}$ to a decimal.

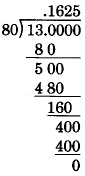
Thirteen point zero zero zero zero is being divided by eighty, using long division method. See the longdesc for a full description.

$0.16 \frac{1}{4} = 0.1625.$

Exercises

For the following problems, perform each indicated operation.

$1.84 + 7.11$

$8.95$

$15.015 - 6.527$

$4.904 - 2.67$

$2.234$

$156.33 - 24.095$

$.0012 + 1.53 + 5.1$

$6.6312$

$44.98 + 22.8 - 12.76$

$5.0004 - 3.00004 + 1.6837$

$3.68406$

$1.11 + 12.1212 - 13.131313$

$4.26 \cdot 3.2$

$13.632$

$2.97 \cdot 3.15$

$23.05 \cdot 1.1$

$25.355$

$5.009 \cdot 2.106$

$0.1 \cdot 3.24$

$0.324$

$100 \cdot 12.008$

$1000 \cdot 12.008$

$12, 008$

$10, 000 \cdot 12.008$

$75.642 \div 18.01$

$4.2$

$51.811 \div 1.97$

$0.0000448 \div 0.014$

$0.0032$

$0.129516 \div 1004$

For the following problems, convert each decimal fraction to a fraction.

$0.06$

$\frac{3}{50}$

$0.115$

$3.7$

$3 \frac{7}{10}$

$48.1162$

$712.00004$

$712 \frac{1}{25000}$

For the following problems, convert each fraction to a decimal fraction. If the decimal form is nonterminating,round to 3 decimal places.

$\frac{5}{8}$

$\frac{9}{20}$

$0.45$

$15 \div 22$

$\frac{7}{11}$

$0.636$

$\frac{2}{9}$

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Basic mathematics review. OpenStax CNX. Jun 06, 2012 Download for free at http://cnx.org/content/col11427/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Basic mathematics review' conversation and receive update notifications?

Ask

©flickr: Tim	Hazard Quiz By Royalle Moore Start Quiz
	6 AP Key Terms 06 The Skeletal System By OpenStax Start Key Terms
©flickr: Gisela	Electrocardiogram Quiz By Anonymous User Start Quiz
	2 Pharmacology Nervous System Essay By Rohini Ajay Start Test
	8 AP 08 Appendicular Skeleton Essay By OpenStax Start Flashcards
	3 Pharmacology Excl. Nervous System MCQ By Rohini Ajay Start Quiz
	1 Pharmacology Nervous System MCQ By Rohini Ajay Start Quiz
	1 Microbiology Final 1 By Madison Christian Start Quiz
	3 Biology 03 Biological Macromolecules MCQ By OpenStax Start Quiz
	American Politics MCQ By Nicole Bartels Start Quiz