| << Chapter < Page | Chapter >> Page > |
We shall study detailed aspect of circular motion under constant angular acceleration in a separate module.
A flywheel of a car is rotating at 300 revolutions per minute. Find its angular speed in radian per second.
Flywheel covers angular displacement of "2π" in one revolution. Therefore, the angular speed in "radian/second" is :
Hence, option (b) is correct.
A particle is rotating along a circle of radius 0.1 m at an angular speed of π rad/s. The time period of the rotation is :
The time period of rotation is :
Note : The input of radius is superfluous here.
Hence, option (b) is correct.
A particle is rotating at constant speed along a circle of radius 0.1 m, having a time period of 1 second. Then, angular speed in "revolution/s" is :
The time period of rotation is :
Rearranging, the angular speed is :
Converting to in the unit of revolution per second, the angular speed is :
Hence, option (a) is correct.
A particle is moving with a constant angular speed "ω" along a circle of radius "r" about a perpendicular axis passing through the center of the circle. If " n " be the unit vector in the positive direction of axis of rotation, then linear velocity is given by :
The linear velocity is given by the following vector cross product,
We know that a change in the order of operands in cross product reverses the resulting vector. Hence,
Further, it is given in the question that positive axial direction has the unit vector "n". But, the plane of motion is perpendicular to axis of rotation. Hence, velocity is not aligned in the direction of unit vector n .
Hence, options (a) and (b) are correct.
The figure shows the plot of angular displacement and time of a rotating disc. Corresponding to the segments marked on the plot, the direction of rotation is as :
Angular displacement
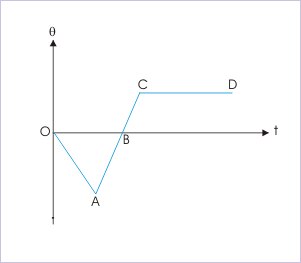
(a) disk rotates in clockwise direction in the segments OA and AB.
(b) disk rotates in clockwise direction in the segment OA, but in anti-clockwise direction in the segment AB.
(c) disk rotates in anti-clockwise direction in the segment BC.
(d) disk rotates in anti-clockwise direction in the segment CD.
The direction of rotation is determined by the sign of angular velocity. In turn, the sign of angular velocity is determined by the sign of the slope on angular displacement - time plot. The sign of slope is negative for line OA, positive for line AC and zero for line CD.
The positive angular velocity indicates anti-clockwise rotation and negative angular velocity indicates clockwise rotation. The disk is stationary when angular velocity is zero.
Hence, options (b) and (c) are correct.
A particle moves along a circle in xy-plane with center of the circle as origin. It moves from position Q(1, √3) to R(-1, √3) as shown in the figure. The angular displacement is :
Angular displacement

In order to find angular displacement, we need to find initial and final angular positions. From the geometry,
Angular displacement
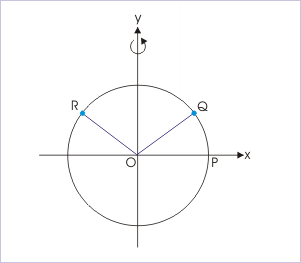
Similarly,
Thus, angular displacement is :
Hence, option (c) is correct.
Select the correct statement(s) :
(a) The direction of angular velocity is tangential to the circular path.
(b) The direction of angular velocity and centripetal acceleration are radial towards the center of the circle.
(c) The linear velocity, angular velocity and centripetal accelerations are mutually perpendicular to each other.
(d) The direction of angular velocity is axial.
The direction of linear velocity is normal to radial direction. The direction of centripetal acceleration is radial. The direction of angular velocity is axial. See the figure.
Angular motion
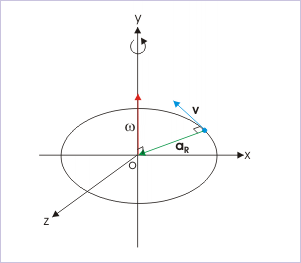
Clearly, the three directions are mutually perpendicular to each other.
Hence, options (c) and (d) are correct.
The magnitude of centripetal acceleration is given by :
The centripetal acceleration is given by :
The linear speed "v" is related to angular speed by the relation,
Substituting this in the expression of centripetal acceleration, we have :
We need to evaluate fourth cross product expression to know whether its modulus is equal to the magnitude of centripetal acceleration or not. Let the cross product be equal to a vector " A ". The magnitude of vector " A " is :
For circular motion, the angle between linear and angular velocity is 90°. Hence,
Substituting for " ω", we have :
The modulus of the expression, therefore, is equal to the magnitude of centripetal acceleration.
Note : The vector cross product "| ω X v |” is the vector expression of centripetal force.
Hence, options (a) and (d) are correct.

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?