10.5 There and back again - an exploration of the liouville  (Page 8/10)

where $f\left(t\right)=\frac{\sin \sqrt{{\mu }_1}(1-t)-\sin \sqrt{{\mu }_1}t}{\sin \sqrt{{\mu }_1}}$ and $f^{\text{'}}\left(t\right)=\frac{-\sqrt{{\mu }_1}\left(\cos ,\sqrt{{\mu }_1},(1-t),+,\cos ,\sqrt{{\mu }_1},t\right)}{\sin \sqrt{{\mu }_1}}$ . To compare, in the rest of this section, some results will be discussed for other $q\left(t\right)$ or $\rho \left(x\right)$ which can be written much more simply.

$q$ and $\rho$ that satisfy the Liouville Transformation

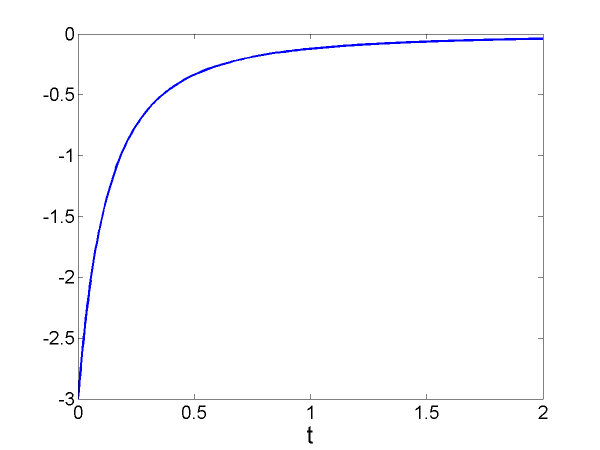
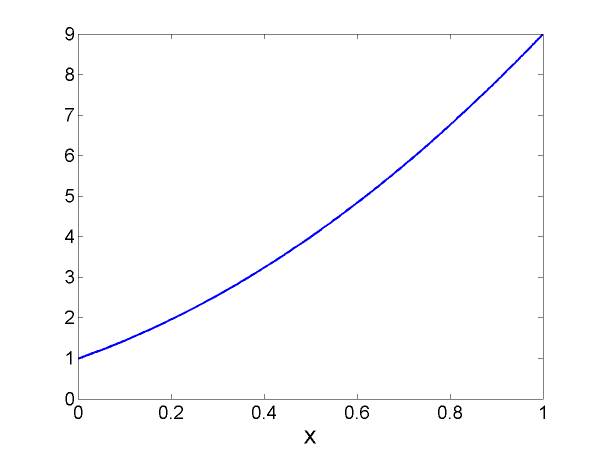
The potential function and the corresponding mass density function

respectively, satisfy [link] , the Liouville transformation. The graphs of $q\left(t\right)$ and $\rho \left(x\right)$ are given in [link] and [link] , respectively. In comparing these graphs with the results from the potential function [link] , one difference to note is that the $q$ in [link] has a domain of $t\in [0,2]$ . This potential is not even , over any interval of positive $t$ values, which is another difference from the potential from [link] . As a result of these differences, it is not surprising that the $\rho$ in [link] has a different graph from all the computed $\rho$ from [link] for the various values of ${\mu }_1$ , but there are some similarities. This $\rho$ in closed form, has $\rho \left(0\right)=1$ as we required for our results in "Numerical Results" . The graph of this $\rho$ in [link] has another similarity to the computed $\rho$ when ${\mu }_1=17.1$ because that graph also shows $\rho \left(1\right)=9$ , however, the shape of the graphs between those two endpoints is quite different.

The spacing of the eigenvalues produced by [link] , calculated by spectral discretization, can be seen in [link] . For comparison, in addition to the computed eigenvalues from these equations, the eigenvalues for the string of uniform density are graphed as small black dots in [link] . The expected eigenvalues from [link] are the same as the eigenvalues for the string of uniform density, except for the first one. The eigenvalues from [link] show the same quadratic behavior as is seen in [link] , but these eigenvalues increase very slowly compared to the eigenvalues for the uniform mass density.

Next is an example of a density function in closed form from Euler.

Example from Euler

Leonhard Euler found the wave equation has a general solution of

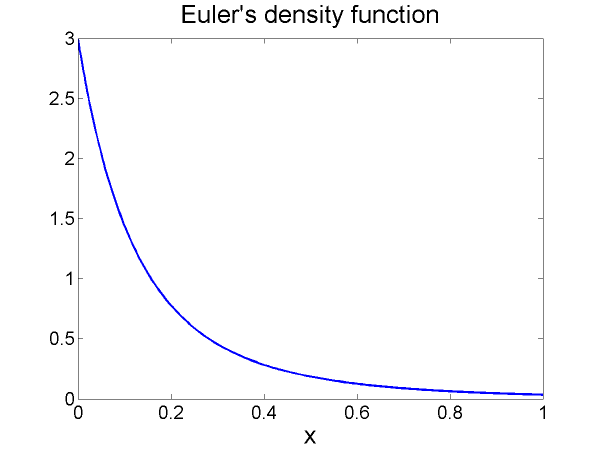
where $c_0\equiv \sqrt{\frac{T}{{\sigma }_0}}$ when the "line density" isgiven by $\sigma \left(x\right)=\frac{{\sigma }_0}{{\left(1,+,\frac{x}{\alpha }\right)}^4}$ [link] . Euler's analysis showed the frequencies of this string would be $v_k=\frac{k}{2L}\left(1,+,\frac{L}{\alpha }\right)\sqrt{\frac{T}{{\sigma }_0}}$ . In order to produce figures which would compare easily to the results from the previous section, the following constants were chosen: ${\sigma }_0=3$ and $\alpha =\frac{1}{2}$ . The resultant graph of $\sigma \left(x\right)$ , which is very different from the other mass density graphs in this paper, can be seen in [link] , and the first 256 frequencies are graphed in [link] .

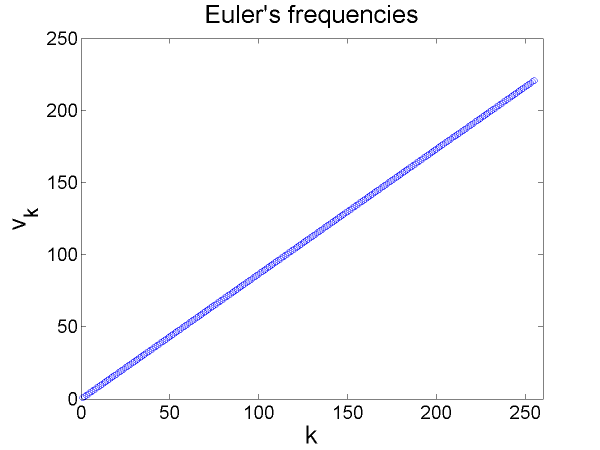
The relationship between eigenvalues, ${\lambda }_k$ , and frequencies, $v_k$ , is given by ${\lambda }_k={\left(2,\pi ,v_k\right)}^2$ . Using this relationship, in [link] , the exact eigenvalues for $k=1$ to 256 have been graphed as blue circles. To compare the results from this set of equations to the others in this module, the eigenvalues were computed for this $\sigma \left(x\right)$ using spectral discretization with $N=256$ . These computed eigenvalues are also graphed in [link] , each marked with a green 'x'. The error between the eigenvalues from the frequency function and the computed eigenvalues is graphed in [link] , which shows the first 100 eigenvalues are computed with reasonable accuracy. For comparison, in addition to the exact and computed eigenvalues from Euler's equations, the eigenvalues for the string of uniform density are graphed as black dots in [link] . The eigenvalues from Euler's equations still show the same quadratic behavior as the other examples we have seen, but these eigenvalues increase very rapidly compared to the eigenvalues for the uniform mass density.