| << Chapter < Page | Chapter >> Page > |
Locate and label each of the given fractions on a number line:
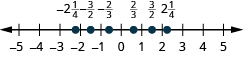
Locate and label each of the given fractions on a number line:
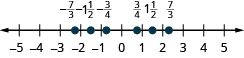
We can use the inequality symbols to order fractions. Remember that means that is to the right of on the number line. As we move from left to right on a number line, the values increase.
Order each of the following pairs of numbers, using or
ⓐ

ⓑ

ⓒ

ⓓ

Order each of the following pairs of numbers, using or
Order each of the following pairs of numbers, using or
In the following exercises, name the fraction of each figure that is shaded.
In the following exercises, shade parts of circles or squares to model the following fractions.
In the following exercises, use fraction circles to make wholes, if possible, with the following pieces.
In the following exercises, name the improper fractions. Then write each improper fraction as a mixed number.
In the following exercises, draw fraction circles to model the given fraction.
In the following exercises, rewrite the improper fraction as a mixed number.
In the following exercises, rewrite the mixed number as an improper fraction.
In the following exercises, use fraction tiles or draw a figure to find equivalent fractions.
How many sixths equal one-third?
How many eighths equal three-fourths?
How many fourths equal three-halves?
In the following exercises, find three fractions equivalent to the given fraction. Show your work, using figures or algebra.
In the following exercises, plot the numbers on a number line.
In the following exercises, order each of the following pairs of numbers, using or
Music Measures A choreographed dance is broken into counts. A count has one step in a count, a count has two steps in a count and a count has three steps in a count. How many steps would be in a count? What type of count has four steps in it?
Music Measures Fractions are used often in music. In time, there are four quarter notes in one measure.
Baking Nina is making five pans of fudge to serve after a music recital. For each pan, she needs cup of walnuts.
Give an example from your life experience (outside of school) where it was important to understand fractions.
Answers will vary.
Explain how you locate the improper fraction on a number line on which only the whole numbers from through are marked.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
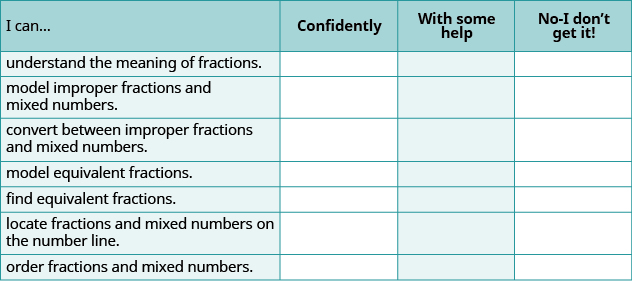
ⓑ If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?