| << Chapter < Page | Chapter >> Page > |
As we saw above, we can represent functions in tables. Conversely, we can use information in tables to write functions, and we can evaluate functions using the tables. For example, how well do our pets recall the fond memories we share with them? There is an urban legend that a goldfish has a memory of 3 seconds, but this is just a myth. Goldfish can remember up to 3 months, while the beta fish has a memory of up to 5 months. And while a puppy’s memory span is no longer than 30 seconds, the adult dog can remember for 5 minutes. This is meager compared to a cat, whose memory span lasts for 16 hours.
The function that relates the type of pet to the duration of its memory span is more easily visualized with the use of a table. See [link] . http://www.kgbanswers.com/how-long-is-a-dogs-memory-span/4221590. Accessed 3/24/2014.
| Pet | Memory span in hours |
|---|---|
| Puppy | 0.008 |
| Adult dog | 0.083 |
| Cat | 16 |
| Goldfish | 2160 |
| Beta fish | 3600 |
At times, evaluating a function in table form may be more useful than using equations. Here let us call the function The domain of the function is the type of pet and the range is a real number representing the number of hours the pet’s memory span lasts. We can evaluate the function at the input value of “goldfish.” We would write Notice that, to evaluate the function in table form, we identify the input value and the corresponding output value from the pertinent row of the table. The tabular form for function seems ideally suited to this function, more so than writing it in paragraph or function form.
Given a function represented by a table, identify specific output and input values.
| 1 | 2 | 3 | 4 | 5 | |
| 8 | 6 | 7 | 6 | 8 |
When we input 2 into the function our output is 6. When we input 4 into the function our output is also 6.
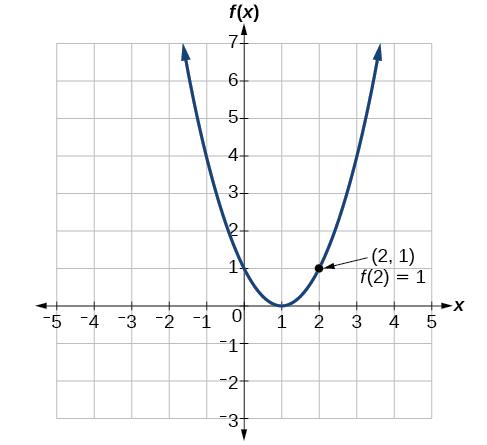
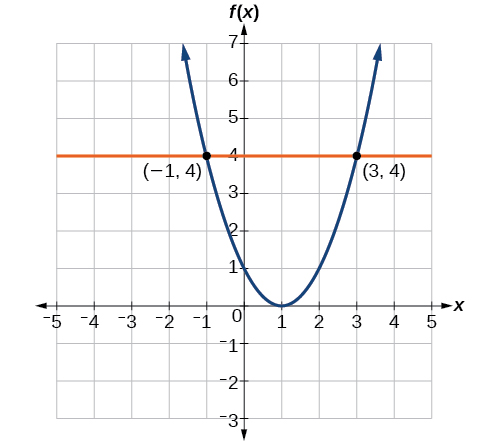
Evaluating a function using a graph also requires finding the corresponding output value for a given input value, only in this case, we find the output value by looking at the graph. Solving a function equation using a graph requires finding all instances of the given output value on the graph and observing the corresponding input value(s).

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?