| << Chapter < Page | Chapter >> Page > |
Khan academy video on point-slope and standard form
There are many different methods of specifying the requirements for determining the equation of a straight line. One option is to find the equation of a straight line, when two points are given.
Assume that the two points are and , and we know that the general form of the equation for a straight line is:
So, to determine the equation of the line passing through our two points, we need to determine values for (the gradient of the line) and (the -intercept of the line). The resulting equation is
where are the co-ordinates of either given point.
This is an example of a set of simultaneous equations, because we can write:
We now have two equations, with two unknowns, and .
Now, to make things a bit easier to remember, substitute [link] into [link] :
If you are asked to calculate the equation of a line passing through two points, use:
to calculate and then use:
to determine the equation.
For example, the equation of the straight line passing through and is given by first calculating
and then substituting this value into
to obtain
Then substitute to obtain
So, passes through and .
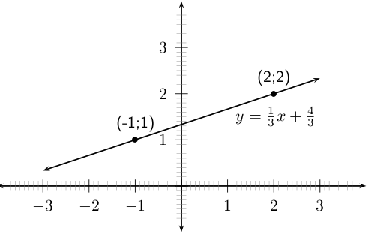
Find the equation of the straight line passing through and .
The equation of the straight line that passes through and is .
Another method of determining the equation of a straight-line is to be given one point, , and to be told that the line is parallel or perpendicular to another line. If the equation of the unknown line is and the equation of the second line is , then we know the following:
Once we have determined a value for , we can then use the given point together with:
to determine the equation of the line.
For example, find the equation of the line that is parallel to and that passes through .
First we determine , the slope of the line we are trying to find. Since the line we are looking for is parallel to ,
The equation is found by substituting and into:

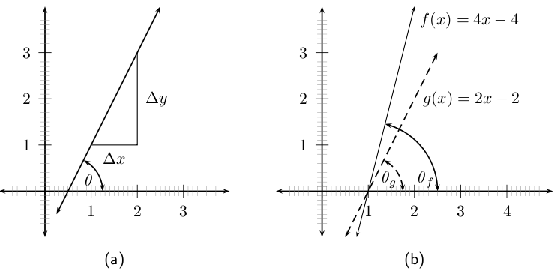
In [link] (a), we see that the line makes an angle with the -axis. This angle is known as the inclination of the line and it is sometimes interesting to know what the value of is.
Firstly, we note that if the gradient changes, then the value of changes ( [link] (b)), so we suspect that the inclination of a line is related to the gradient. We know that the gradient is a ratio of a change in the -direction to a change in the -direction.
But, in [link] (a) we see that
For example, to find the inclination of the line , we know

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 11 maths' conversation and receive update notifications?