Introduction and key concepts

Introduction

This chapter focuses on vectors. We will learn what is a vector and how it differs from everyday numbers. We will also learn how to add, subtract and multiply them and where they appear in Physics.

Are vectors Physics? No, vectors themselves are not Physics. Physics is just a description of the world around us. To describe something we need to use a language. The most common language used to describe Physics is Mathematics. Vectors form a very important part of the mathematical description of Physics, so much so that it is absolutely essential to master the use of vectors.

Scalars and vectors

In Mathematics, you learned that a number is something that represents a quantity. For example if you have 5 books, 6 apples and 1 bicycle, the 5, 6, and 1 represent how many of each item you have.

These kinds of numbers are known as scalars .

Scalar

A scalar is a quantity that has only magnitude (size).

An extension to a scalar is a vector, which is a scalar with a direction. For example, if you travel 1 km down Main Road to school, the quantity 1 km down Main Road is a vector. The “ 1 km ” is the quantity (or scalar) and the “ down Main Road ” gives a direction.

In Physics we use the word magnitude to refer to the scalar part of the vector.

Vectors

A vector is a quantity that has both magnitude and direction.

A vector should tell you how much and which way .

For example, a man is driving his car east along a freeway at $100\mathrm{km}·\mathrm{h}{}^{-1}$ . What we have given here is a vector – the velocity. The car is moving at $100\mathrm{km}·\mathrm{h}{}^{-1}$ (this is the magnitude) and we know where it is going – east (this is the direction). Thus, we know the speed and direction of the car. These two quantities, a magnitude and a direction, form a vector we call velocity.

Notation

Vectors are different to scalars and therefore have their own notation.

Mathematical representation

There are many ways of writing the symbol for a vector. Vectors are denoted by symbols with an arrow pointing to the right above it. For example, $\overrightarrow{a}$ , $\overrightarrow{v}$ and $\overrightarrow{F}$ represent the vectors acceleration, velocity and force, meaning they have both a magnitude and a direction.

Sometimes just the magnitude of a vector is needed. In this case, the arrow is omitted. In other words, $F$ denotes the magnitude of the vector $\overrightarrow{F}$ .

Graphical representation

Vectors are drawn as arrows. An arrow has both a magnitude (how long it is) and a direction (the direction in which it points). The starting point of a vector is known as the tail and the end point is known as the head .

Directions

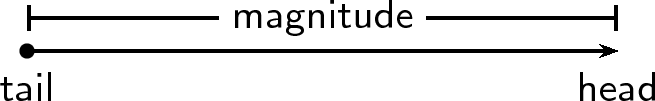
There are many acceptable methods of writing vectors. As long as the vector has a magnitude and a direction, it is most likely acceptable. These different methods come from the different methods of expressing a direction for a vector.

Relative directions

The simplest method of expressing direction is with relative directions: to the left, to the right, forward, backward, up and down.

Compass directions

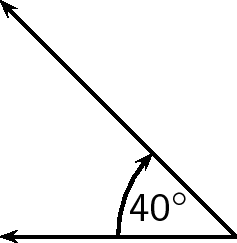
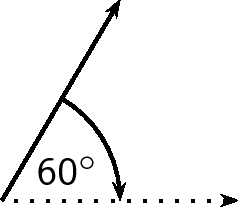
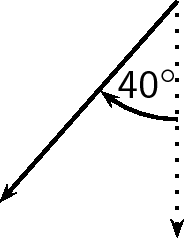
Another common method of expressing directions is to use the points of a compass: North, South, East, and West. If a vector does not point exactly in one of the compass directions, then we use an angle. For example, we can have a vector pointing $40{}^{\circ }$ North of West. Start with the vector pointing along the West direction: Then rotate the vector towards the north until there is a $40{}^{\circ }$ angle between the vector and the West. The direction of this vector can also be described as: W $40{}^{\circ }$ N (West $40{}^{\circ }$ North); or N $50{}^{\circ }$ W (North $50{}^{\circ }$ West)

Bearing

The final method of expressing direction is to use a bearing . A bearing is a direction relative to a fixed point.

Given just an angle, the convention is to define the angle with respect to the North. So, a vector with a direction of $110{}^{\circ }$ has been rotated clockwise $110{}^{\circ }$ relative to the North. A bearing is always written as a three digit number, for example $275{}^{\circ }$ or $080{}^{\circ }$ (for $80{}^{\circ }$ ).

Scalars and vectors

1. Classify the following quantities as scalars or vectors:
   1. 12 km
   2. 1 m south
   3. $2\mathrm{m}·{\mathrm{s}}^{-1}$ , $45{}^{\circ }$
   4. $075{}^{\circ }$ , 2 cm
   5. $100\mathrm{k}·{\mathrm{h}}^{-1}$ , $0{}^{\circ }$
2. Use two different notations to write down the direction of the vector in each of the following diagrams:

   1. 

   2. 

   3. 

Drawing vectors

In order to draw a vector accurately we must specify a scale and include a reference direction in the diagram. A scale allows us totranslate the length of the arrow into the vector's magnitude. For instance if one chose a scale of 1 cm = 2 N (1 cm represents 2 N), aforce of 20 N towards the East would be represented as an arrow 10 cm long. A reference direction may be a line representing a horizontal surface or the points of a compass.

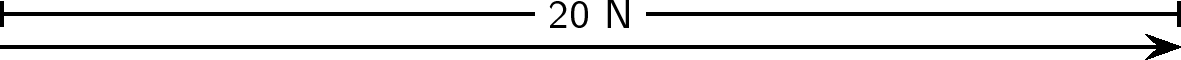
Method: Drawing Vectors

1. Decide upon a scale and write it down.
2. Determine the length of the arrow representing the vector, by using the scale.
3. Draw the vector as an arrow. Make sure that you fill in the arrow head.
4. Fill in the magnitude of the vector.

Drawing vectors

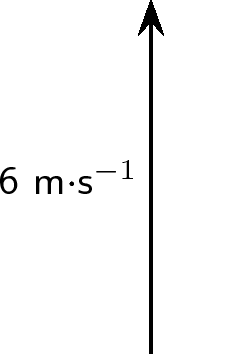
Draw each of the following vectors to scale. Indicate the scale that you have used:

1. 12 km south
2. 1,5 m N $45{}^{\circ }$ W
3. $1\mathrm{m}·\mathrm{s}{}^{-1}$ , $20{}^{\circ }$ East of North
4. $50\mathrm{km}·\mathrm{h}{}^{-1}$ , $085{}^{\circ }$
5. 5 mm, $225{}^{\circ }$