| << Chapter < Page | Chapter >> Page > |
In engineering, we often deal with the idea of an action occurring at a point. Whether it be a force at a point in spaceor some other signal at a point in time, it becomes worth while to develop some way of quantitatively defining this. This leads usto the idea of a unit impulse, probably the second most important function, next to the complex exponential, in this systems and signalscourse.
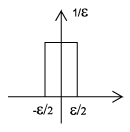
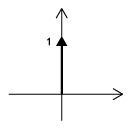
The Dirac delta function , often referred to as the unit impulse or delta function, is the function thatdefines the idea of a unit impulse in continuous-time. Informally, this function is one that is infinitesimally narrow, infinitely tall, yet integrates toone. Perhaps the simplest way to visualize this is as a rectangular pulse from to with a height of . As we take the limit of this setup as approaches 0, we see that the width tends to zero and the height tends to infinity as the total area remains constant at one.The impulse function is often written as .
Below is a brief list a few important properties of the unit impulse without going into detail of their proofs.
The continuous time unit impulse function, also known as the Dirac delta function, is of great importance to the study of signals and systems. Informally, it is a function with infinite height ant infinitesimal width that integrates to one, which can be viewed as the limiting behavior of a unit area rectangle as it narrows while preserving area. It has several important properties that will appear again when studying systems.

Notification Switch
Would you like to follow the 'Signals and systems' conversation and receive update notifications?