| << Chapter < Page | Chapter >> Page > |
Deur te gebruik wat ons geleer het omtrent trigonometriese funksies, kan ons nou eenvoudige trigonometriese vergelykings oplos. Ons gebruik ook die beginsels van Equations and Inequalities om ons te help om trigonometriese vergelykings op te los.
Los die volgende trigonometriese vergeyking op:
Trigonometrie is waarskynlik in antieke beskawings uitgevind om praktiese probleme, byvoorbeeld in die bou- en konstruksiebedryf, asook navigasie met behulp van sterre, op te los. In hierdie afdeling sal ons wys hoe trigonometrie gebruik kan word om 'n paar ander praktiese probleme op te los.
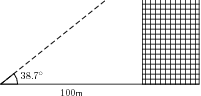
'n Eenvoudige taak is om die hoogte van 'n gebou te vind met behulp van trigonometrie. Ons sou net 'n maatband van die dak kon laat sak, maar dit is onprakties (en gevaarlik) by hoë geboue. Dit is baie meer sinvol om 'n afstand op die grond te meet en trigonometrie te gebruik om die hoogte van die gebou te vind.
[link] toon 'n gebou waarvan ons nie die hoogte weet nie. Ons het 100 m weg van die gebou gestap en die hoek van die grond tot by die top van die gebou gemeet . Hierdie hoek is . Ons noem hierdie hoek die hoogtehoek . Soos jy kan sien van [link] , het ons nou 'n reghoekige driehoek. Omdat ons weet wat die lengte van een sy en 'n hoek is, kan ons die hoogte van die driehoek bereken, wat die hoogte van die gebou is wat ons probeer vind.
As ons kyk na die figuur, sien ons dat ons met die teenoorstaande en die aangrensende sy van die hoogtehoek werk en ons kan skryf:
'n Blok woonstelle is 100m weg van 'n selfoontoring. Iemand staan by . Hulle meet die hoek van na die bopunt van die toring en dit is 62 . Dit is die hoogtehoek. Dan meet hulle die hoek van af na die basis van die toring en dit is 34 . Dit is die dieptehoek. Wat is die hoogte van die selfoontoring korrek tot 1 desimale plek?
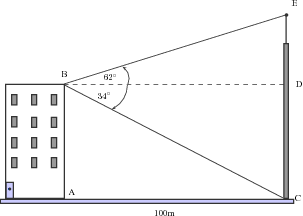
Om die hoogte van 'n toring te vind, hoef ons net die lengte van en te vind. Ons sien dat en beide reghoekige driehoeke is. Vir elkeen van die driehoeke het ons 'n hoek en ons het die lengte . Dus kan ons die sye van die driehoeke bereken.
Dit word vir ons gegee dat die lengte van 100m is. is 'n reghoek, dus .
Gebruik jou sakrekenaar om te vind dat . Deur dit te gebruik, vind ons dat m.
Ons het die hoogte van die toring .
Kaarte en planne is gewoonlik skaaltekeninge. Dit beteken hulle is 'n presiese kopie van die regte ding, maar gewoonlik kleiner. Dus word net lengtes verander, maar al die hoeke is dieselfde. Ons kan dus hierdie idee gebruik om kaarte en planne te gebruik deur inligting van die werklike wêreld by te voeg.
'n Skip op pad na die Kaapstadhawe bereik punt A op die kaart, reg suid van Pretoria en reg oos van Kaapstad. As die afstand vanaf Kaapstad na Pretoria 1000km is, gebruik trigonometrie om uit te vind hoe ver oos die skip van Kaapstad is, en vind op hierdie manier die skaal van die kaart.

Ons weet reeds die afstand tussen Kaapstad en in blokke van die gegewe kaart, is 5 blokke. Dus, as ons bereken hoeveel kilometers hierdie afstand is, kan ons bereken hoeveel kilometers elke blok verteenwoordig, en dan het ons die skaal van die kaart.
Laat ons Kaapstad aandui met en Pretoria met . Ons kan sien dat die driehoek reghoekig is. Verder sien ons en afstand is beide 5 blokke. Dit is dus 'n gelykbenige driehoek en .
Om die skaal uit te werk, sien ons dat
Mnr Nkosi het 'n motorhuis by sy huis, en hy besluit hy wil 'n sinkdak aan die kant van sy motorhuis aanlas. Die motorhuis is 4m hoog, en die plaat vir die dak is 5m lank. As hy die dak teen 'n hoek van wil hê, hoe hoog moet hy die muur, , wat die dak ophou, bou? Gee die antwoord tot 2 desimale plekke.
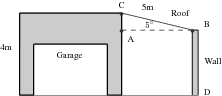
Ons sien dat die driehoek 'n reghoekige driehoek is. Aangesien ons een sy en 'n hoek van die driehoek het, kan ons bereken. Die hoogte van die muur is die hoogte van die motorhuis minus .
As =5m, en hoek , dan
Dus het ons dat die hoogte van die muur .

Notification Switch
Would you like to follow the 'Siyavula textbooks: wiskunde (graad 10) [caps]' conversation and receive update notifications?