| << Chapter < Page | Chapter >> Page > |
In grades 10 and 11 you have learnt about linear functions and quadratic functions as well as the hyperbolic functions and exponential functions and many more. In grade 12 you are expected to demonstrate the ability to work with various types of functions and relations including the inverses of some functions and generate graphs of theinverse relations of functions, in particular the inverses of:
.
A function is a relation for which there is only one value of corresponding to any value of . We sometimes write , which is notation meaning ' is a function of '. This definition makes complete sense when compared to our real world examples — each person has only one height, so height is a function of people; on each day, in a specific town, there is only one average temperature.
However, some very common mathematical constructions are not functions. For example, consider the relation . This relation describes a circle of radius 2 centred at the origin, as in [link] . If we let , we see that and thus either or . Since there are two values which are possible for the same value, the relation is not the graph a function.
There is a simple test to check if a relation is a function, by looking at its graph. This test is called the vertical line test . If it is possible to draw any vertical line (a line of constant ) which crosses the graph of the relation more than once, then the relation is not a function. If more than one intersection point exists, then the intersections correspond to multiple values of for a single value of .
We can see this with our previous example of the circle by looking at its graph again in [link] .
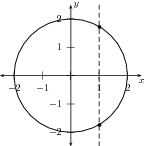
We see that we can draw a vertical line, for example the dotted line in the drawing, which cuts the circle more than once. Therefore this is not a function.
| 1 | 2 | 3 | 4 | |
| 22500 | 22000 | 21500 | 21000 |
In grade 10 you were introduced to the notation used to "name" a function. In a function , is called the dependent variable , because the value of depends on what you choose as . We say is the independent variable , since we can choose to be any number. Similarly if , then is the independent variable and is the function name. If and you are ask to determine , then you have to work out the value for when . For example,

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 12 maths' conversation and receive update notifications?