| << Chapter < Page | Chapter >> Page > |
We can express the relationship between logarithmic form and its corresponding exponential form as follows:
Note that the base is always positive.
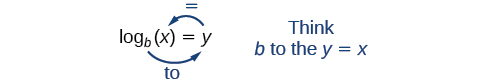
Because logarithm is a function, it is most correctly written as using parentheses to denote function evaluation, just as we would with However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written without parentheses, as Note that many calculators require parentheses around the
We can illustrate the notation of logarithms as follows:

Notice that, comparing the logarithm function and the exponential function, the input and the output are switched. This means and are inverse functions.
A logarithm base of a positive number satisfies the following definition.
For
where,
Also, since the logarithmic and exponential functions switch the and values, the domain and range of the exponential function are interchanged for the logarithmic function. Therefore,
Can we take the logarithm of a negative number?
No. Because the base of an exponential function is always positive, no power of that base can ever be negative. We can never take the logarithm of a negative number. Also, we cannot take the logarithm of zero. Calculators may output a log of a negative number when in complex mode, but the log of a negative number is not a real number.
Given an equation in logarithmic form convert it to exponential form.
Write the following logarithmic equations in exponential form.
First, identify the values of Then, write the equation in the form
Here, Therefore, the equation is equivalent to
Here, Therefore, the equation is equivalent to
Write the following logarithmic equations in exponential form.
To convert from exponents to logarithms, we follow the same steps in reverse. We identify the base exponent and output Then we write
Write the following exponential equations in logarithmic form.
First, identify the values of Then, write the equation in the form
Here, and Therefore, the equation is equivalent to
Here, and Therefore, the equation is equivalent to
Here, and Therefore, the equation is equivalent to

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?