| << Chapter < Page | Chapter >> Page > |
The composition evaluates to angle values lying in the interval .
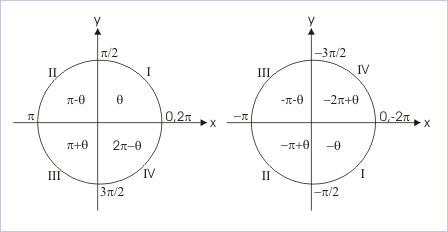
Let us consider adjacent intervals such that all tangent values are included once. Such intervals are (π/2, 3π/2), (3π/2, 5π/2) etc on the right side and (-3π/2, -π/2), (-5π/2, -3π/2) etc on the left side of the principal interval.
Tangent function

The new interval represents second and third quadrants. The angle x, corresponding to positive acute angle θ, lies in third quadrant. Then,
Value diagrams
Hence,
In order to find expression corresponding to negative angle interval , we estimate from the tangent plot that an angle corresponding to a positive acute angle, θ, in the principal interval lies in second negative quadrant. Therefore,
Hence,
Combining three results,
| x+π; x∈ (-3π/2, -π/2)
tan⁻¹ tanx = | x; x∈ (-π/2, π/2)| x-π; x∈ (π/2, 3π/2)
We can similarly find expressions for other intervals.
Using three expressions obtained above, we can draw plot of the composition function. We have extended the plot, using the fact that composition is a periodic function with a period of π. The equation of plot, which is equivalent to plot y=x shifted by π towards right is :
The equation of plot, which is equivalent to plot y=x shifted by π towards left is :
These results are same as obtained earlier. It means that nature of plot is same in the adjacent intervals.
Tangent inverse of tangent
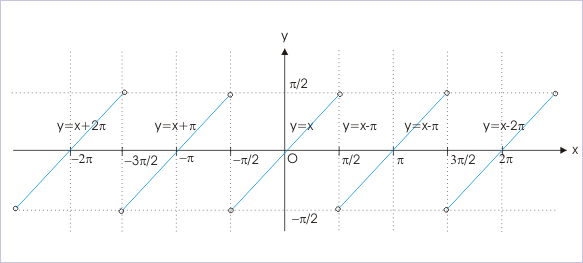
We see that graph of composition is discontinuous. Its domain is . Its range is . The function is periodic with period π.
The composition evaluates to angle values lying in the interval .
Let us consider adjacent intervals such that all cosine values are included once. Such intervals are [π/2, 3π/2] – {π}, [3π/2, 5π/2]– {2π} etc on the right side and [-3π/2, -π/2] – {-π}, [-5π/2, -3π/2]– {-2π} etc on the left side of the principal interval.
Cosecant function

The new interval lies in second and third quadrants. The angle x corresponding to positive acute angle θ, lies in second quadrant. Then,
Value diagrams

Hence,
In order to find expression corresponding to negative angle interval , we estimate from the cosecant plot that an angle corresponding to a positive acute angle, θ, in the principal interval lies in third negative quadrant. Therefore,
Hence,
Combining three results,
|- π-x; x∈[-3π/2, -π/2] – {-π}cosec⁻¹ cosecx = | x; x∈[-/2, π/2]-{0}| π- x; x∈[π/2, 3π/2] – {π}
We can similarly find expressions for other intervals.
Using three expressions obtained above, we can draw plot of the composition function. We have extended the plot, using the fact that composition is a periodic function with a period of 2π. The equation of plot, which is equivalent to plot y=x shifted by 2π towards right, is :
The equation of plot, which is equivalent to plot y=x shifted by 2π towards left, is :
Cosecant inverse of cosecant
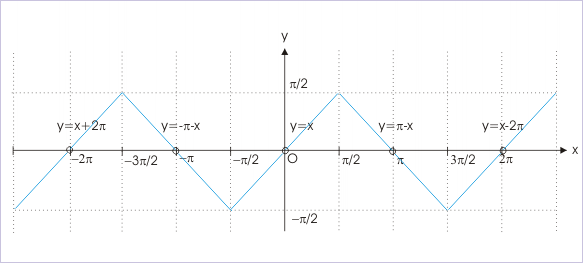
We see that graph of composition is discontinuous. Its domain is . Its range is . The function is periodic with period 2π.

Notification Switch
Would you like to follow the 'Functions' conversation and receive update notifications?