13.3 Matched filter detector  (Page 3/4)

Of course, there is not necessarily exactly one instance of a target signal in a given signal. There could be one instance, more than one instance, or no instance of a target signal. Therefore, it is often more practical to identify all shifts corresponding to local maxima that are above a certain threshold.

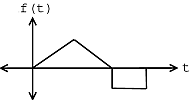
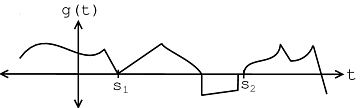
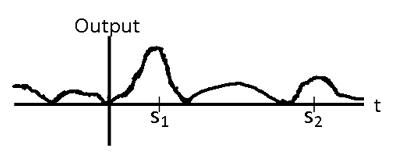
The signal in [link] contains an instance of the template signal seen in [link] beginning at time $t=s_1$ as shown by the plot in [link] . Therefore,

$$s_1={argmax}_{t\in \mathbb{R}}\left|〈\frac{f}{\left|\right|f\left|\right|},,,\frac{w{S}_{t}g}{\left|\right|w{S}_{t}g\left|\right|}〉\right|.$$

Pattern signal

Longer signal

Absolute value of output

Got questions? Get instant answers now!

Practical applications

Image detection

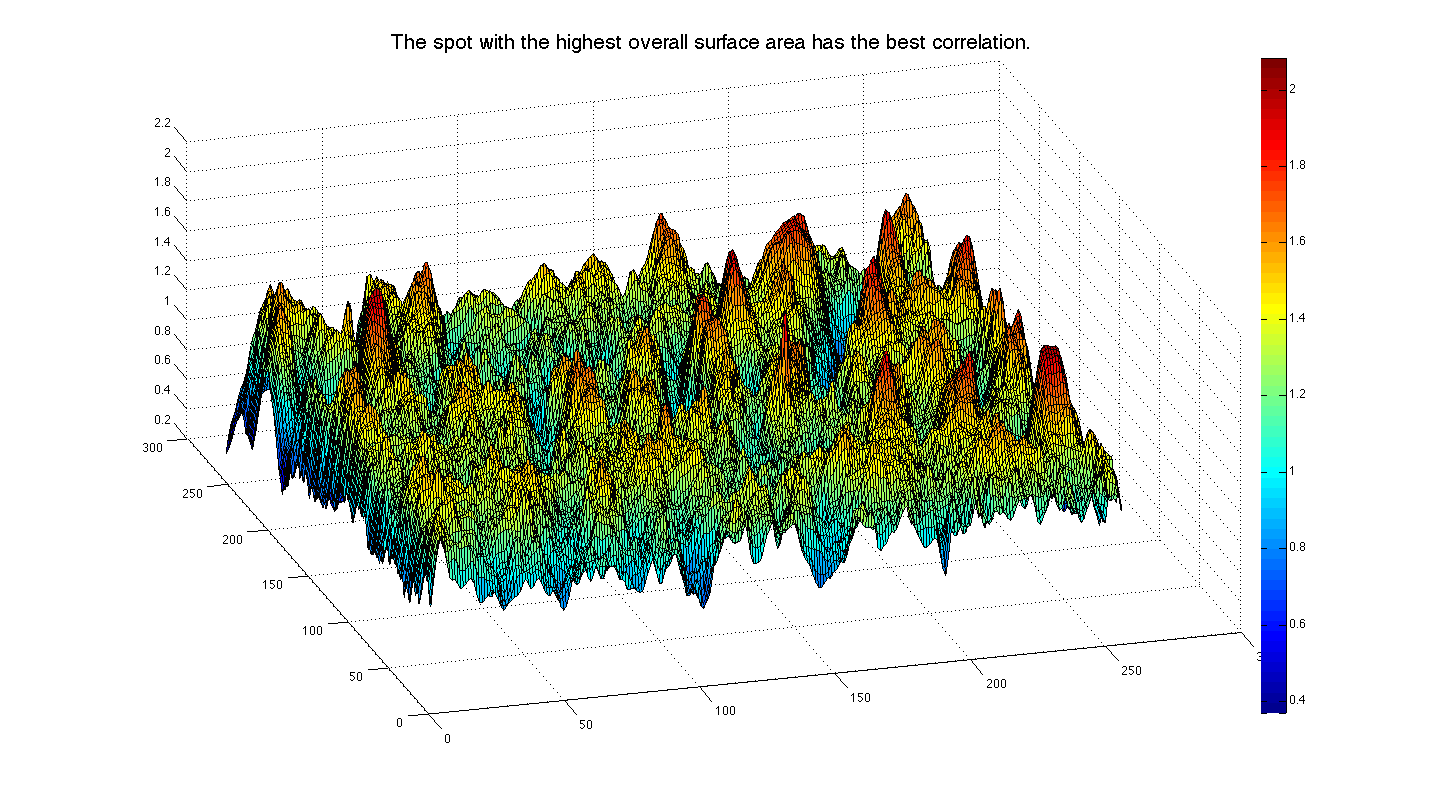
Matched Filtering is used in image processing to detect a template image within a reference image. This has real-word applications in verifying fingerprints for security or in verifying someone's photo. As a simple example, we can turn to the ever-popular "Where's Waldo?" books (known as Wally in the UK!), where the reader is tasked with finding the specific face of Waldo/Wally in a confusing background rife with look-alikes! If we are given the template head and a reference image, we can run a two dimensional convolution of the template image across the reference image to obtain a three dimensional convolution map, [link] , where the height of the convolution map is determined by the degree of correlation, higher being more correlated. Finding our target then becomes a matter of determining the spot where the local surface area is highest. The process is demonstrated in [link] . In the field of image processing, this matched filter-based process is known as template matching .

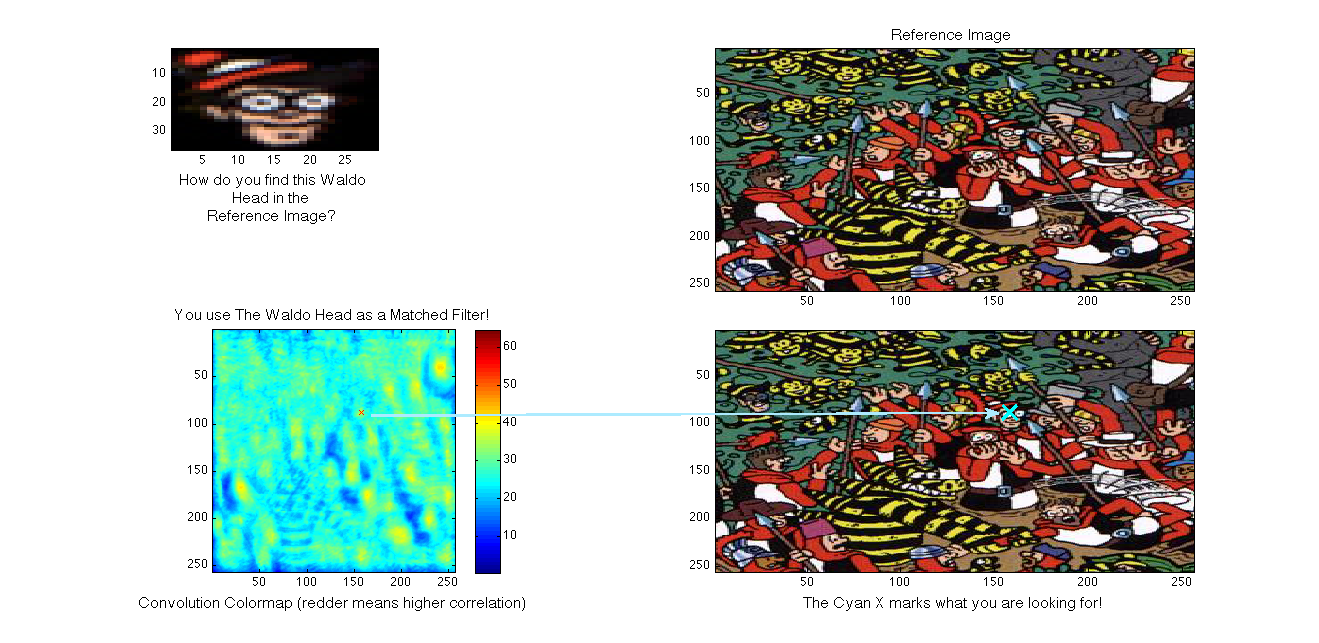
then we could easily develop a program to find the closest resemblance to the image of Waldo's head in the largerpicture. We would simply implement our same match filter algorithm: take the inner products at each shift and seehow large our resulting answers are. This idea was implemented on this same picture for a Signals and Systems Project at Rice University (click the link to learn more).

Communications systems

Matched filter detectors are also commonly used in Communications Systems . In fact, they are the optimal detectors in Gaussian noise. Signals in the real-world are often distorted by the environment around them, sothere is a constant struggle to develop ways to be able to receive a distorted signal and then be able to filter itin some way to determine what the original signal was. Matched filters provide one way to compare a receivedsignal with two possible original ("template") signals and determine which one is the closest match to the receivedsignal.