| << Chapter < Page | Chapter >> Page > |


Theorem 4 The angle subtended by an arc at the centre of a circle is double the size of the angle subtended by the same arc at the circumference of the circle.
Proof :
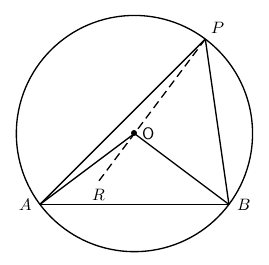
Consider a circle, with centre and with and on the circumference. Draw a chord . Draw radii and . Select any point on the circumference of the circle. Draw lines and . Draw and extend to . The aim is to prove that . (exterior angle = sum of interior opp. angles) But, ( is an isosceles ) Similarly, . So,
Theorem 5 The angles subtended by a chord at the circumference of a circle on the same side of the chord are equal.
Proof :
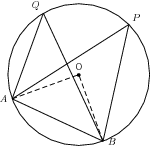
Consider a circle, with centre . Draw a chord . Select any points and on the circumference of the circle, such that both and are on the same side of the chord. Draw lines , , and . The aim is to prove that .
Theorem 6 (Converse of Theorem [link] ) If a line segment subtends equal angles at two other points on the same side of the line, then these four points lie on a circle.
Proof :
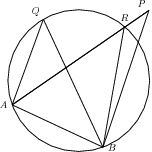
Consider a line segment , that subtends equal angles at points and on the same side of . The aim is to prove that points , , and lie on the circumference of a circle. By contradiction. Assume that point does not lie on a circle drawn through points , and . Let the circle cut (or extended) at point .
the assumption that the circle does not pass through , must be false, and , , and lie on the circumference of a circle.
Cyclic quadrilaterals are quadrilaterals with all four vertices lying on the circumference of a circle. The vertices of a cyclic quadrilateral are said to be concyclic .
Theorem 7 The opposite angles of a cyclic quadrilateral are supplementary.
Proof :
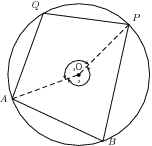
Consider a circle, with centre . Draw a cyclic quadrilateral . Draw and . The aim is to prove that and .
Theorem 8 (Converse of Theorem [link] ) If the opposite angles of a quadrilateral are supplementary, then the quadrilateral is cyclic.
Proof :
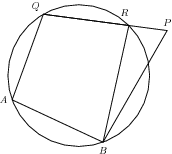
Consider a quadrilateral , such that and . The aim is to prove that points , , and lie on the circumference of a circle. By contradiction. Assume that point does not lie on a circle drawn through points , and . Let the circle cut (or extended) at point . Draw .
the assumption that the circle does not pass through , must be false, and , , and lie on the circumference of a circle and is a cyclic quadrilateral.

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 12 maths' conversation and receive update notifications?