Introduction, circle geometry

Introduction

Discussion : discuss these research topics

Research one of the following geometrical ideas and describe it to your group:

1. taxicab geometry,
2. spherical geometry,
3. fractals,
4. the Koch snowflake.

Circle geometry

Terminology

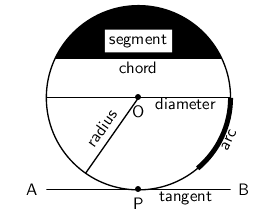
The following is a recap of terms that are regularly used when referring to circles.

• arc An arc is a part of the circumference of a circle.
• chord A chord is defined as a straight line joining the ends of an arc.
• radius The radius, $r$ , is the distance from the centre of the circle to any point on the circumference.
• diameter The diameter is a special chord that passes through the centre of the circle. The diameter is the straight line from a point on the circumference to another point on the circumference, that passes through the centre of the circle.
• segment A segment is the part of the circle that is cut off by a chord. A chord divides a circle into two segments.
• tangent A tangent is a line that makes contact with a circle at one point on the circumference. ( $AB$ is a tangent to the circle at point $P$ ).

Axioms

An axiom is an established or accepted principle. For this section, the following are accepted as axioms.

1. The Theorem of Pythagoras, which states that the square on the hypotenuse of a right-angled triangle is equal to the sum of the squares on the other two sides. In $▵ABC$ , this means that ${\left(AB\right)}^2+{\left(BC\right)}^2={\left(AC\right)}^2$

   

2. A tangent is perpendicular to the radius, drawn at the point of contact with the circle.

Theorems of the geometry of circles

A theorem is a general proposition that is not self-evident but is proved by reasoning (these proofs need not be learned for examination purposes).

Theorem 1 The line drawn from the centre of a circle, perpendicular to a chord, bisects the chord.

Proof :

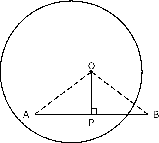
Consider a circle, with centre $O$ . Draw a chord $AB$ and draw a perpendicular line from the centre of the circle to intersect the chord at point $P$ . The aim is to prove that $AP$ = $BP$

1. $▵OAP$ and $▵OBP$ are right-angled triangles.
2. $OA=OB$ as both of these are radii and $OP$ is common to both triangles.

Apply the Theorem of Pythagoras to each triangle, to get:

However, $OA=OB$ . So,

This means that $OP$ bisects $AB$ .

Theorem 2 The line drawn from the centre of a circle, that bisects a chord, is perpendicular to the chord.

Proof :

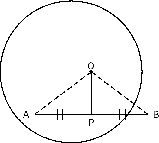
Consider a circle, with centre $O$ . Draw a chord $AB$ and draw a line from the centre of the circle to bisect the chord at point $P$ . The aim is to prove that $OP\perp AB$ In $▵OAP$ and $▵OBP$ ,

1. $AP=PB$ (given)
2. $OA=OB$ (radii)
3. $OP$ is common to both triangles.

$\therefore ▵OAP\equiv ▵OBP$ (SSS).

Theorem 3 The perpendicular bisector of a chord passes through the centre of the circle.

Proof :

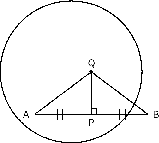
Consider a circle. Draw a chord $AB$ . Draw a line $PQ$ perpendicular to $AB$ such that $PQ$ bisects $AB$ at point $P$ . Draw lines $AQ$ and $BQ$ . The aim is to prove that $Q$ is the centre of the circle, by showing that $AQ=BQ$ . In $▵OAP$ and $▵OBP$ ,

1. $AP=PB$ (given)
2. $\angle QPA=\angle QPB$ ( $QP\perp AB$ )
3. $QP$ is common to both triangles.

$\therefore ▵QAP\equiv ▵QBP$ (SAS). From this, $QA=QB$ . Since the centre of a circle is the only point inside a circle that has points on the circumference at an equal distance from it, $Q$ must be the centre of the circle.