| << Chapter < Page | Chapter >> Page > |
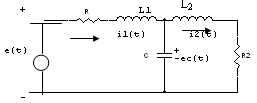
H.5_2
Điện thế ngang qua tụ ec(t), các dòng điện trong các cuộn cảm i1(t) và i2(t) được xem như là các biến số trạng thái.
Các phương trình trạng thái có được bằng cách viết điện thế ngang qua các cuộn cảm và dòng trong tụ.
(5.4)
(5.5)
(5.6)
Sắp xếp lại các hệ số hằng, các phương trình trạng thái được viết dưới dạng chính tắc như sau:
(5.7)
Hầu hết các hệ tự kiểm đều có chứa các bộ phận cơ khí cũng như các bộ phận điện. Trên quan điểm toán học, sự mô tả các bộ phận cơ và điện thì tương đương nhau. Thật vậy, ta có thể chứng minh rằng một bộ phận cơ khí thường là một bản sao của một bộ phận điện tương đương, và ngược lại. Dĩ nhiên, sự tương đương chỉ trên ý nghĩa toán học. Hai hệ thống thì tương đương nhau nếu chúng được diễn tả bằng các phương trình giống nhau.
Sự chuyển động của các bộ phận cơ có thể là tịnh tiến, quay hoặc phối hợp cả hai. Các phương trình chỉ ra chuyển động của các hệ cơ thì thường được viết một cách trực tiếp hay gián tiếp từ định luật chuyển động của Newton.
Chuyển động tịnh tiến được định nghĩa như là một chuyển động dời chổ dọc theo một đường thẳng. Các biến được dùng mô tả chuyển động tịnh tiến là gia tốc, vận tốc và độ dời.
Định luật Newton chứng tỏ rằng tổng đại số các lực tác động lên một cäú thãø theo một phương đã cho thì bằng tích số của khối lượng của cäú thãø và gia tốc của nó theo cùng phương đó.
lực = Ma(5.8)
Trong đó: M là khối lượng và a là gia tốc.
Trong chuyển động tịnh tiến, các bộ phận sau đây thường được đưa vào:
Khối lượng được xem như là một đặc trưng của một bộ phận tích trữ động năng trong chuyển động tịnh tiến. Nó tương đương với cuộn cảm của mạch điện. Nếu W là trọng lượng của cäú thãø, thì M được cho bởi:
(5.9)
g: Gia tốc trọng trường.
Trong hệ thống SI, đơn vị của M là kg, của g là m/s2; của lực là Newton(N).
f(t)My(t)
Hình H.5_3: Hệ thống lực- khối lượng.
HìnhH. 5_3 mô tả vị trí mà ở đó một lực tác động lên một cäú thãø có khối lượng M.
Phương trình được viết:
(5.10)
Trong đó y(t) chỉ độ dời; v(t): vận tốc; a(t): gia tốc.
Tất cả được tham chiếu theo hướng của lực áp dụng.
Một cách tổng quát, là xo được xem như là một bộ phận tích trữ thế năng. Nó tương đương với tụ điện trong các mạch điện.
Trong thực tế, lò xo tuyến tính có thể là một lò xo thực sự, hoặc một dây courroir. Dù tất cả các lò xo đều phi tuyến ở vài vùng hoạt động. Nhưng, nếu sự biến dạng của lò xo nhỏ, trạng thái của nó có thể được xấp xỉ hoá (approximated) bằng một hệ thức tuyến tính:
f(t)= Ky(t)(5.11)
Với K là hằng số lò xo, hoặc hằng số đàn hồi (Stifness)
Đơn vị của K: N/m
Phương trình (5.11) cho thấy lực tác động lên lò xo thì tỷ lệ trực tiếp với độ dời (độ biến dạng) của lò xo. Mô hình biểu diển một bộ phận lò xo tuyến tính vẽ ở hình H.5_4.
y(t)f(t)
H.5_4: Hệ thống lực-lò xo.
Nếu lò xo có mang trước một sức căng T thì (5.12) sẽ được cải biến thành:

Notification Switch
Would you like to follow the 'Cơ sở tự động học' conversation and receive update notifications?