| << Chapter < Page | Chapter >> Page > |
The Least Mean Squares (LMS) Algorithm can be used in a range of Digital Signal Processing applications such as echo cancellation and acoustic noise reduction.
This laboratory shows how to design a model of LMS Noise Cancellation using Simulink and run it on a Texas Instruments C6000 DSP.
Intermediate - Assumes prior knowledge of MATLAB and Simulink. It also requires a theoretical understanding of matrices and the LMS algorithm.
This laboratory was originally developed using the following hardware and software:
You will now start with a simple Simulink model and run it to see how it works.
Open the AcousticNoiseCancellation.mdl
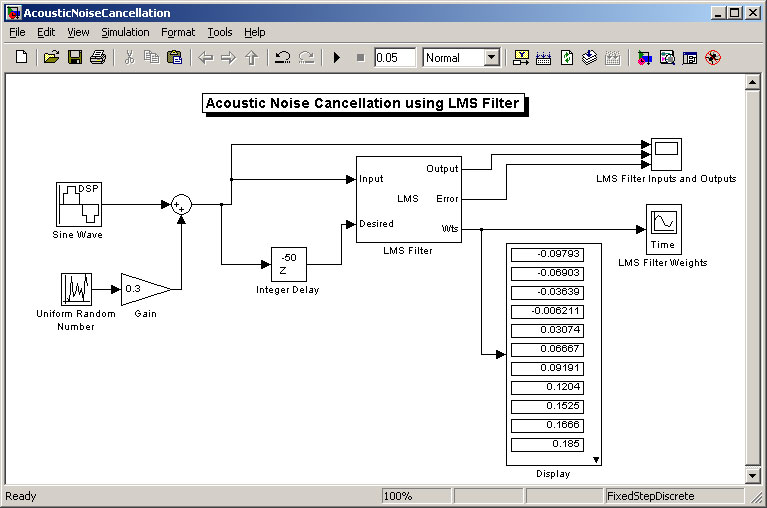
Run the model.
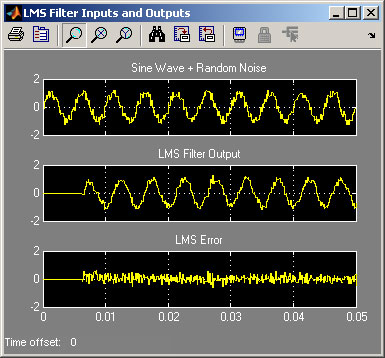
The output from the LMS Filter starts at zero and grows slowly. Initially, some of the sine wave information is lost as LMS Error.
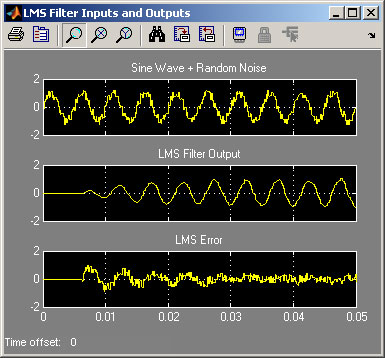
The LMS Filter Weights all start at zero and take several iterations to reach their final values.
The critical variable in the LMS Filter is the “Step size (mu)”. This sets the rate of convergence of the LMS filter.
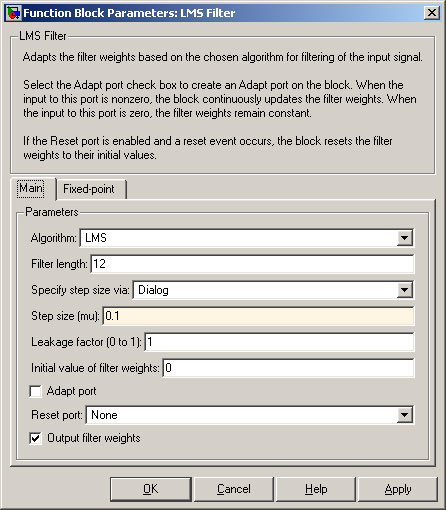
Double-click on the “LMS Filter” block and change the “Step size (mu) to 0.1
Run the model.
When the “Step size (mu)” is increased, LMS algorithm converges more quickly, but at the expense of granularity – the LMS Filter Output is not as smooth.
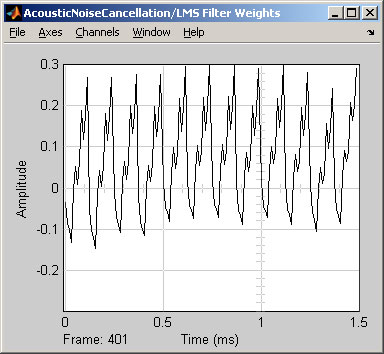
Note that the filter weights (coefficients) do not attain smooth values, as would be the case for smaller values of Step size (mu).
Part of the Acoustic Noise Algorithm is the delay. The delay should ideally be at least half a wavelength so the two inputs to the LMS Filter have different random noise.

Notification Switch
Would you like to follow the 'From matlab and simulink to real-time with ti dsp's' conversation and receive update notifications?