| << Chapter < Page | Chapter >> Page > |
Computer must not only be able to carry out computations, they must be able to do them quickly and efficiently. There are several data representations, typically for integers, real numbers, characters, and logical values.
A numeral system is a collection of symbols used to represent small numbers, together with a system of rules for representing larger numbers. Each numeral system uses a set of digits. The number of various unique digits, including zero, that a numeral system uses to represent numbers is called base or radix.
b basic symbols (or digits) corresponding to natural numbers between 0 and b − 1 are used in the representation of numbers.
To generate the rest of the numerals, the position of the symbol in the figure is used. The symbol in the last position has its own value, and as it moves to the left its value is multiplied by b.
We write a number in the numeral system of base b by expressing it in the form
N(b), with n+1 digit for integer and m digits for fractional part, represents the sum:
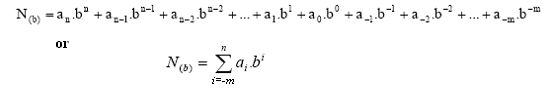
in the decimal system. Note that is the digit from the position of
Decimal, Binary, Octal and Hexadecimal are common used numeral system. The decimal system has ten as its base. It is the most widely used numeral system, because humans have four fingers and a thumb on each hand, giving total of ten digit over both hand.
Switches, mimicked by their electronic successors built of vacuum tubes, have only two possible states: "open" and "closed". Substituting open=1 and closed=0 yields the entire set of binary digits. Modern computers use transistors that represent two states with either high or low voltages. Binary digits are arranged in groups to aid in processing, and to make the binary numbers shorter and more manageable for humans.Thus base 16 (hexadecimal) is commonly used as shorthand. Base 8 (octal) has also been used for this purpose.
Decimal System
Decimal notation is the writing of numbers in the base-ten numeral system, which uses various symbols (called digits) for no more than ten distinct values (0, 1, 2, 3, 4, 5, 6, 7, 8 and 9) to represent any number, no matter how large. These digits are often used with a decimal separator which indicates the start of a fractional part, and with one of the sign symbols + (positive) or − (negative) in front of the numerals to indicate sign.
Decimal system is a place-value system. This means that the place or location where you put a numeral determines its corresponding numerical value. A two in the one's place means two times one or two. A two in the one-thousand's place means two times one thousand or two thousand.
The place values increase from right to left. The first place just before the decimal point is the one's place, the second place or next place to the left is the ten's place, the third place is the hundred's place, and so on.
The place-value of the place immediately to the left of the "decimal" point is one in all place-value number systems. The place-value of any place to the left of the one's place is a whole number computed from a product (multiplication) in which the base of the number system is repeated as a factor one less number of times than the position of the place.

Notification Switch
Would you like to follow the 'Introduction to computer science' conversation and receive update notifications?