2.7 Getalsin  (Page 2/2)

Hierdie is verrykingswerk en as u dit te gevorderd vind, kan dit in 'n later stadium gedoen word. Daar mag wel leerders wees wat die uitdaging sal aanvaar.

Aangesien 3 x en ÷ pas voltooi is, is dit maklik om derdes nou aan te pak.

Gee aan die leerders los vorms van papier en laat hulle vou en meet en self ontdek hoe dit gedoen kan word. Sommige van die leerders sal self weet hoe om nou sesdes te kry. (Slegs verryking)

Die idee van die resep is om die leerders te laat besef dat die gebruik van standaard meeteenhede en houers noodsaaklik is.

Laat die leerders nog voorbeelde noem waar standaard meeteenhede om inhoud te meet daagliks gebruik word, bv. brandstof, melk, meng van bestanddele vir medisyne, voorskrifte vir toediening van medikasie, ens.

Dit is noodsaaklik dat al die verskillende standaard maathouers en skale, asook sand, water en ander voorwerpe om inhoud en massa te meet, in die klas beskikbaar moet wees. Die leerders moet daagliks kan eksperimenteer met hierdie standaard meeteenhede: liter en milliliter en gram en kilogram .

'n Badkamerskaal is nodig om die leerders se massas te bepaal.

Verskillende metodes word gebruik vir die vermenigvuldig- en deelbewerkings, maar indien u van 'n ander metode gebruik maak en die leerders dit beter verstaan, is dit hulle reg om die metode wat hulle verkies, te gebruik.

Dit is noodsaaklik dat baie soortgelyke voorbeelde van die betrokke getalsinne eers mondeling gedoen word, voordat van die leerders verwag kan word om hierdie werkvel te voltooi.

Die volmaak van 'n honderd en die ontbinding van 'n honderd word nou formeel aangeleer. Baie konkrete werk moet vooraf gedoen word. Meer gevorde werk waar 'n tien en 'n honderd gelyktydig oorgedra of ontbind word, moet nie op dieselfde tyd gedoen word nie. Dit sal van die groep se vermoëns afhang of dit net hierna of op 'n baie later stadium gedoen moet word.

Dit bly die opvoeder se keuse of die leerders hulpsyfers by die vertikale bewerkings gaan gebruik.

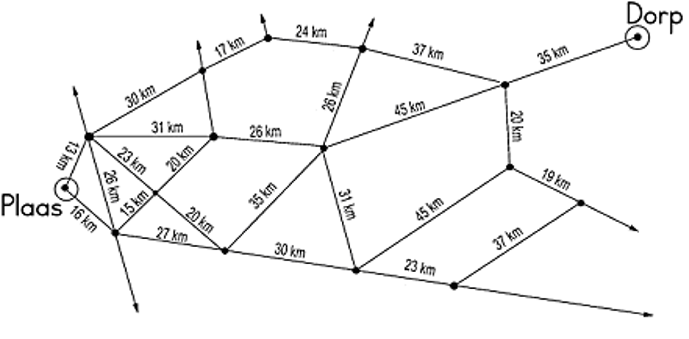
Leerders sal 'n skoon vel papier nodig hê om die korste pad te bereken. Sommige leerders mag dit moeilik vind, maar met 'n bietjie hulp, behoort hulle dit te kan doen.

'n Bespreking oor wat hulle sal sien, afhangende van die rigting waaruit hulle na die huis aangery kom, is nodig voordat die leerders dit kan teken.

Leerders afdeling

Inhoud

Aktiwiteit: getalsin [lu 1.8, lu 1.10]

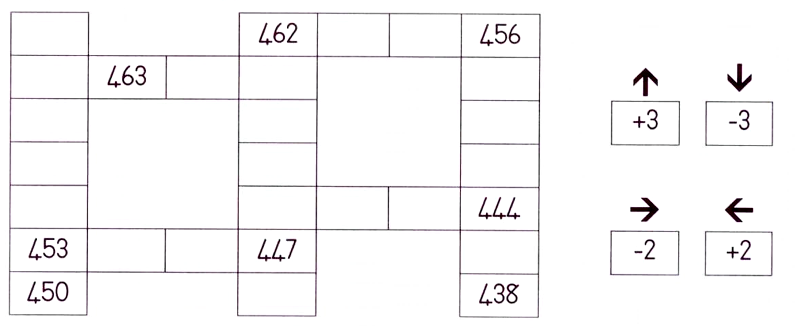
1. Hierdie patrone kan julle help om met groter getalle te werk. Voltooi dit.

2. Kyk hoe Bonnie en Tommie hierdie probleem vir Oupa opgelos het:

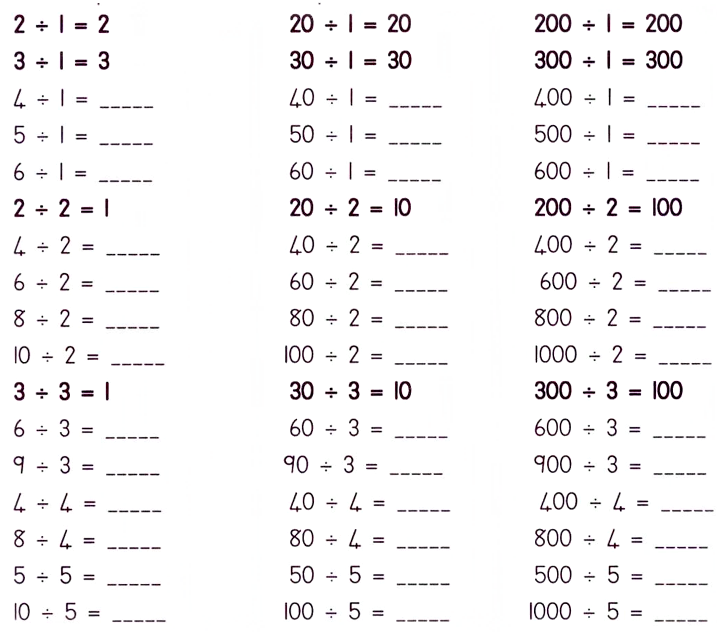
Oupa het 48 varke op die plaas en daar is 4 varkhokke. Hoeveel varke moet hy in elke hok sit?

Getalsin: 48 ÷ 4 = ____________________________

• Help nou vir Ouma op dieselfde manier om hierdie probleem op te los? Ouma het 69 rose gepluk en wil ewe veel in 3 verskillende blompotte sit. Hoeveel moet sy in elke blompot sit?

Getalsin: ____________________________________________________________

Ouma moet ___________________________________________________________

• Doen die bewerkings en gebruik die metode wat jy verkies:

42 ÷ 2 = ______________________________________________

68 ÷ 2 = ______________________________________________

96 ÷ 3 = ______________________________________________

63 ÷ 3 = ______________________________________________

84 ÷ 4 = ______________________________________________

44 ÷ 4 = ______________________________________________

• Skryf 'n storie om by elke getalsin te pas. Doen dan die bewerking.

35 + 42 + 1 7 = _______________________________________

90 - 53 + 12 = _______________________________________

41 x 2 = _____________________________________________

66 ÷ 3 = _____________________________________________

• Bonnie en Tommie het ontdek dat hulle soms genoeg tiene het om 'n groep van honderd vol te maak.

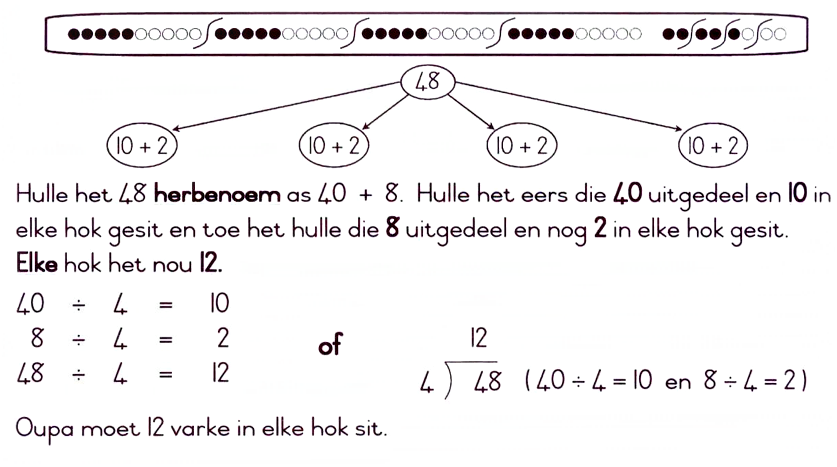
Getalsin: 56 + 62 = ________________________________________

• Doen die bewerkings op die metode waarvan jy die meeste hou:

73 + 55 = _______________________________________________

46 + 63 = _______________________________________________

94 + 23 = _______________________________________________

• Bonnie en Tommie het ook ontdek dat hulle soms nie genoeg tiene het om weg te neem nie en moes toe 'n groep van honderd ontbind.

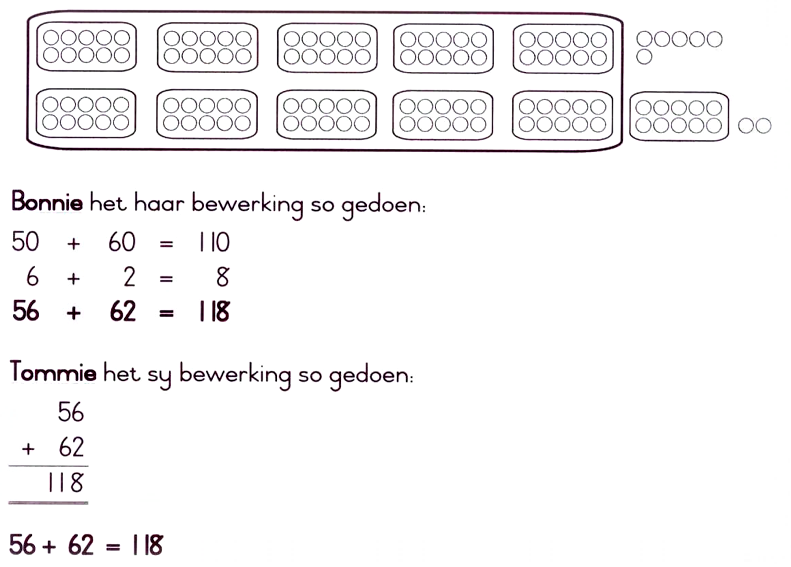
Getalsin: 126 - 32 = ________________________________________

• Doen die bewerkings op die metode waarvan jy die meeste hou:

1 18 - 25 = ________________________________________________

150 - 60 = ________________________________________________

147 - 60 = _________________________________________________

• Vul die antwoorde in:

• Voltooi die syferpad:

• Vul die getalle in wat weggelaat is:

• Hier is 'n padkaart vir Pappa. Daar is verskillende paaie wat hy kon ry om vir Bonnie en Tommie plaas toe te neem, maar watter pad is die kortste?
• Bereken die kortste pad en teken dit op die kaart in.

• Hoeveel km is die kortste pad? ______________________________________

• As Pappa 100 km in 1 uur ry, hoe lank sal dit vir hulle neem om daar te kom?

Dit sal _______________________________________________________________

• Teken Oupa en Ouma se plaas met hulle huis daarop soos julle dit sal sien as julle daar aangery kom.

Assessering

Leeruitkomste 1: Die leerder is in staat om getalle en die verwantskappe daarvan te herken, te beskryf en voor te stel, en om tydens probleemoplossing bevoeg en met selfvertroue te tel, te skat, te bereken en te kontroleer.

Assesseringstandaard 1.8: Dit is duidelik wanneer die leerder die gepaste simbole in berekeninge kan gebruik om probleme op te los;

Assesseringstandaard 1.10: Dit is duidelik wanneer die leerder die volgende tegnieke gebruik:

1.10.1 opbou en afbreek van getalle;

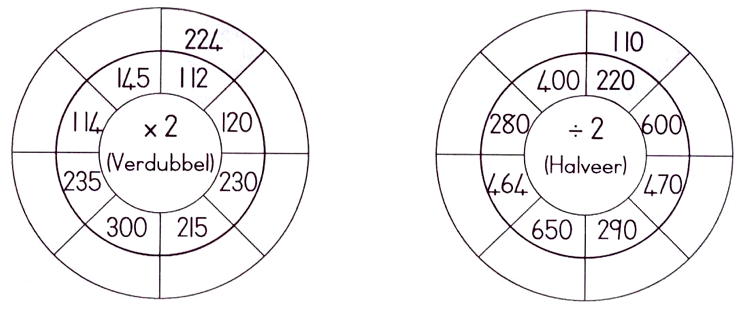
1.10.2 verdubbeling en halvering;

1.10.3 getallelyne;

1.10.4 afronding in tiene.