| << Chapter < Page | Chapter >> Page > |
For convenience, the reference direction like x – axis of the coordinate system serves to represent fixed direction. The angle between reference direction and rotating arm (OP) at any instant is the angular position of the particle (θ).
It must be clearly understood that angular position (θ) is an angle and does not represent the position of the particle by itself. It requires to be paired with radius of the circle (r) along which particle moves in order to specify the position of the particle. Thus, a specification of a position in the reference system will require both “r” and “θ” to be specified.
Relation between distance (s) and angle (θ)
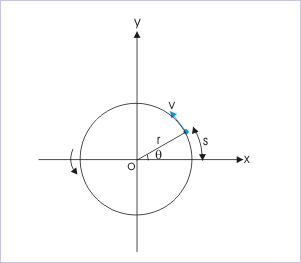
By geometry,
where "s" is the length of the arc subtending angle “θ” at the origin and “r” is the radius of the circle containing the position of the particle. The angular position is measured in “radian”, which has no dimension, being ratio of two lengths. One revolution contains 2π radians. The unit of radian is related to other angle measuring units "degree" and "revolution" as :
1 revolution = 360° = 2π radian
Angular displacement is equal to the difference of angular positions at two instants of rotational motion.
Angular displacement (δθ)

The angular displacement is also measured in “radian” like angular position. In case our measurement of angular position coincides with the reference direction, we can make substitution as given here :
With these substitution, we can simply express angular displacement in terms of angle as :
Angular speed is the ratio of the magnitude of angular displacement and time interval.
This ratio is called average angular velocity, when it is evaluated for finite time interval; and instantaneous angular velocity, when it is evaluated for infinitesimally small period (Δ→0).
The angular velocity is measured in “rad/s”.
Circular motion is completely described when angular position of a particle is given as a function of time like :
For example, tells us the position of the particle with the progress of time. The attributes of circular motion such as angular velocity and acceleration are first and second time derivatives of this function in time. Similarity to pure translational motion is quite obvious here. In pure translational motion, each particle constituting a rigid body follows parallel linear paths. The position of a particle is a function of time, whereby :

Notification Switch
Would you like to follow the 'Physics for k-12' conversation and receive update notifications?