| << Chapter < Page | Chapter >> Page > |
In this section, we examine amplitude modulation and demodulation applications. For transmission purposes, signals are often modulated with a high-frequency carrier. A typical amplitude modulated signal can be described by
where is called the message waveform, which contains the data of interest, and is the carrier wave frequency. Using the fact that
and the frequency shift property of CTFT, one can easily derive the CTFT ofto be
At the receiver, some noisy version of this transmitted signal is received. The signal information resides in the envelope of the modulated signal, and thus an envelope detector can be used to recover the message signal.
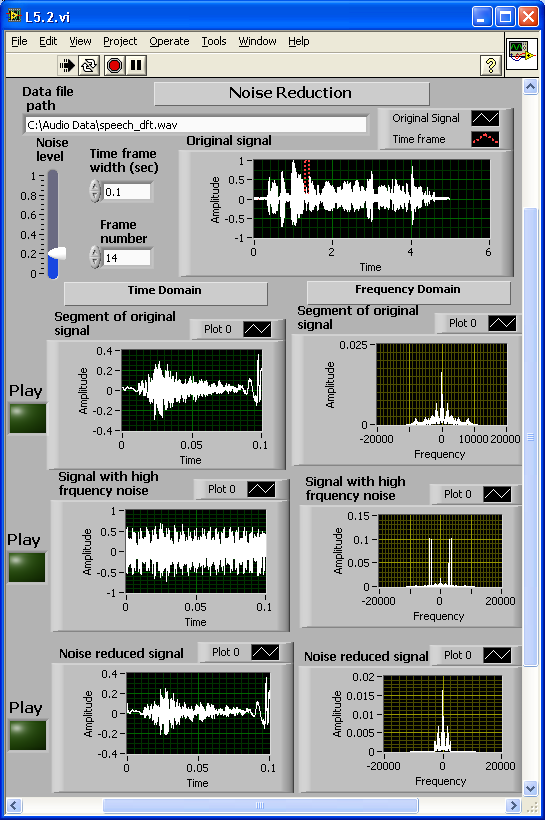
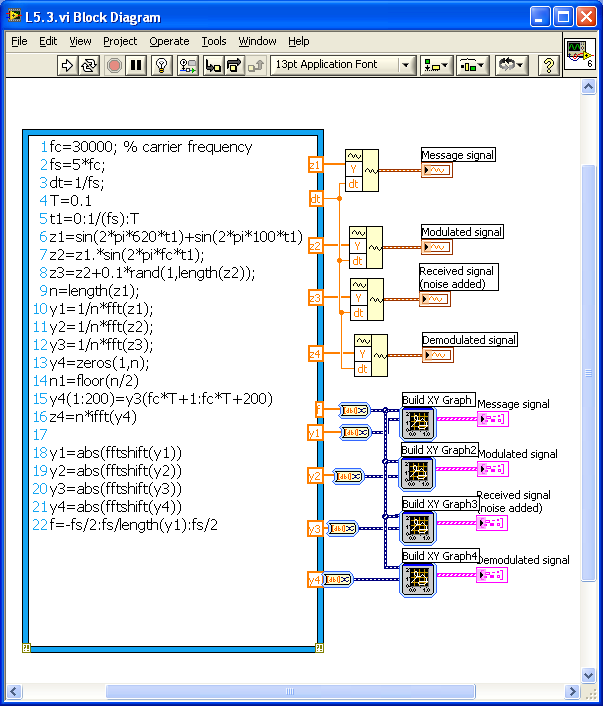
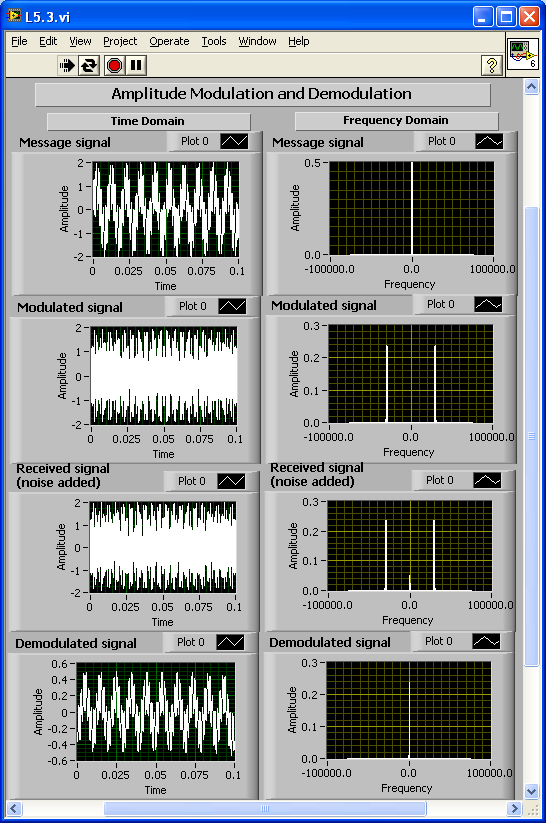
[link] shows the completed block diagram of the amplitude modulation and demodulation system. In this example, use the combination of two sine waves to serve as a message signal. The signal is modulated with a high-frequency carrier, and some random noise is added. The frequency domain versions of the signals can also be observed using the function
fft . As stated in Equation (3), the CTFT of the modulated signal is merely some frequency-shifted version of the original signal. In single sideband (SSB) modulation, only one side of the spectrum is transmitted due to symmetry. That is, just one side of the spectrum is taken and converted into a time signal using the function
ifft .
[link] shows the completed front panel of this system. The Message signal, Modulated signal, Received signal (modulated signal with additional noise) and Demodulated signal are displayed in four waveform graphs in both the time and frequency domains.
Circuit Analysis
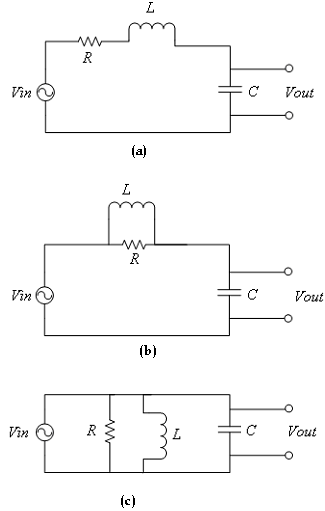
Find and plot the frequency response (both magnitude and phase spectrum) of each of the circuits shown in [link] . Set the values of R, L and C as controls.
Insert Solution Text Here
Morse Coding
Consider a message containing some hidden information. Furthermore, to make it interesting, suppose the message contains a name. Assume that the message was coded using the amplitude modulation scheme as follows [link] :
where and are the (message) signals containing the three letters of the name. More specifically, each of the signals, and , corresponds to a single letter of the alphabet. These letters are encoded using the International Morse Code as indicated below [7]:
Now to encode the letter A, one needs only a dot followed by a dash. That is, only two prototype signals are needed – one to represent the dash and one to represent the dot. Thus, for instance, to represent the letter A, set , where represents the dot signal and the dash signal. Similarly, to represent the letter O, set .
Find the prototype signals
and
in the file
>>load morse
the signals and can be located in the vectors dot and dash, respectively. The hidden signal, which is encoded, per Equation (4), containing the letters of the name, is in the vector Let the three modulation frequencies and be 20, 40 and 80 Hz, respectively.
• Using the amplitude modulation property of the CTFT, determine the three possible letters and the hidden name. (Hint: Plot the CTFT of Use the values of and contained in the file.)
• Explain the strategy used to decode the message. Is the coding technique ambiguous? That is, is there a one-to-one mapping between the message waveforms ( ) and the alphabet letters? Or can you find multiple letters that correspond to the same message waveform?
Insert Solution Text Here
Doppler Effect
The Doppler effect phenomenon was covered in a previous chapter. In this exercise, let us examine the Doppler effect with a real sound wave rather than a periodic signal. The wave file
wavread and produce its upscale and downscale versions. Show the waves in the time and frequency domains (find the CTFT). Furthermore, play the sounds using the LabVIEW function
Play Waveform .
[link] shows a typical front panel for this system.
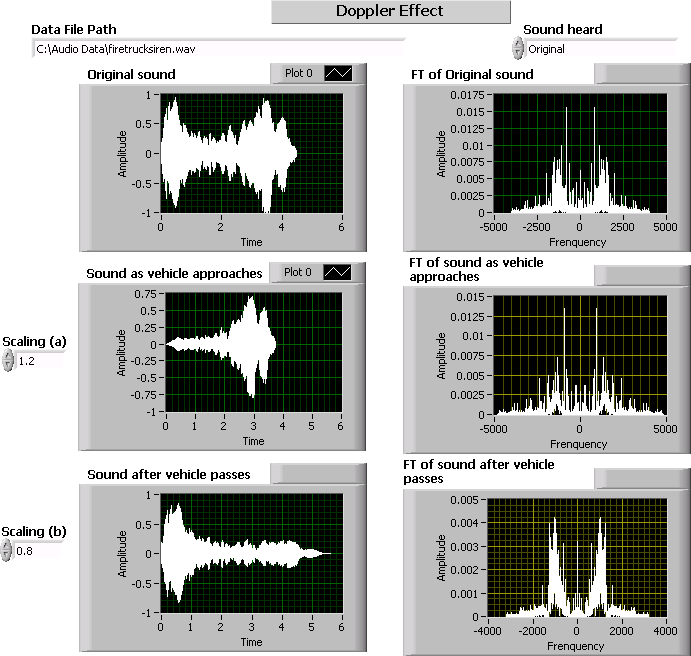
Insert Solution Text Here
Diffraction of Light
The diffraction of light can be described as a Fourier transform [link] . Consider an opaque screen with a small slit being illuminated by a normally incident uniform light wave, as shown in [link] .
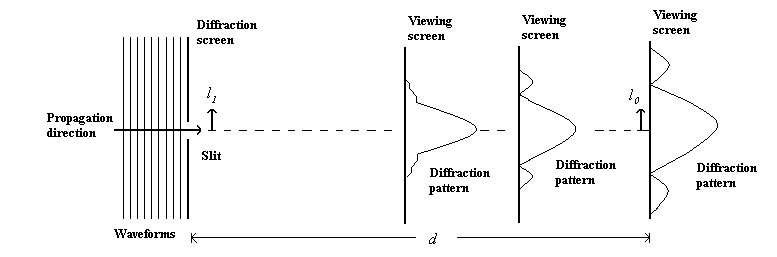
Considering that provides a good approximation for any in the slit, the electric field strength of the light striking the viewing screen can be expressed as [link]
where
= field strength at diffraction screen
= field strength at viewing screen
= constant of proportionality
= wavelength of light
The above integral is in fact Fourier transformation in a different notation. One can write the field strength at the viewing screen as [link]
The intensity of the light at the viewing screen is the square of the magnitude of the field strength. That is,
Insert Solution Text Here

Notification Switch
Would you like to follow the 'An interactive approach to signals and systems laboratory' conversation and receive update notifications?