This module is from Fundamentals of Mathematics by Denny Burzynski and Wade Ellis, Jr. This module discusses how to divide decimals. By the end of the module students should understand the method used for dividing decimals, be able to divide a decimal number by a nonzero whole number and by another, nonzero, decimal number and be able to simplify a division of a decimal by a power of 10.
Section overview
- The Logic Behind the Method
- A Method of Dividing a Decimal By a Nonzero Whole Number
- A Method of Dividing a Decimal by a Nonzero Decimal
- Dividing Decimals by Powers of 10
The logic behind the method
As we have done with addition, subtraction, and multiplication of decimals, we will study a method of division of decimals by converting them to fractions, then we will make a general rule.
We will proceed by using this example: Divide 196.8 by 6.
We have, up to this point, divided 196.8 by 6 and have gotten a quotient of 32 with a remainder of 4. If we follow our intuition and bring down the .8, we have the division
.
Thus,
.
Now, our intuition and experience with division direct us to place the .8 immediately to the right of 32.

From these observations, we suggest the following method of division.
A method of dividing a decimal by a nonzero whole number
Method of dividing a decimal by a nonzero whole number
To divide a decimal by a nonzero whole number:
- Write a decimal point above the division line and directly over the decimal point of the dividend.
- Proceed to divide as if both numbers were whole numbers.
- If, in the quotient, the first nonzero digit occurs to the right of the decimal point, but not in the tenths position, place a zero in each position between the decimal point and the first nonzero digit of the quotient.
Sample set a
Find the decimal representations of the following quotients.
Thus,
.
Check: If
, then
should equal 114.1.
Got questions? Get instant answers now!
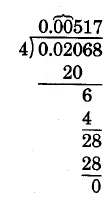
Place zeros in the tenths and hundredths positions. (See Step 3.)
Thus,
.
Got questions? Get instant answers now!
Practice set a
Find the following quotients.
A method of dividing a decimal by a nonzero decimal
Now that we can divide decimals by nonzero whole numbers, we are in a position to divide decimals by a nonzero decimal. We will do so by converting a division by a decimal into a division by a whole number, a process with which we are already familiar. We'll illustrate the method using this example: Divide 4.32 by 1.8.
Let's look at this problem as
.
The divisor is
. We can convert
into a whole number if we multiply it by 10.
But, we know from our experience with fractions, that if we multiply the denominator of a fraction by a nonzero whole number, we must multiply the numerator by that same nonzero whole number. Thus, when converting
to a whole number by multiplying it by 10, we must also multiply the numerator
by 10.


