1. Home
  2. Chemistry
  3. Chemical bonding and molecular
  4. Strengths of ionic and covalent

7.5 Strengths of ionic and covalent bonds  (Page 4/8)

<< Chapter < Page
  Chemistry     Page 4 / 8
Chapter >> Page >

The born-haber cycle

It is not possible to measure lattice energies directly. However, the lattice energy can be calculated using the equation given in the previous section or by using a thermochemical cycle. The Born-Haber cycle    is an application of Hess’s law that breaks down the formation of an ionic solid into a series of individual steps:

  • Δ H f ° , the standard enthalpy of formation of the compound
  • IE , the ionization energy of the metal
  • EA , the electron affinity of the nonmetal
  • Δ H s ° , the enthalpy of sublimation of the metal
  • D , the bond dissociation energy of the nonmetal
  • Δ H lattice , the lattice energy of the compound

[link] diagrams the Born-Haber cycle for the formation of solid cesium fluoride.

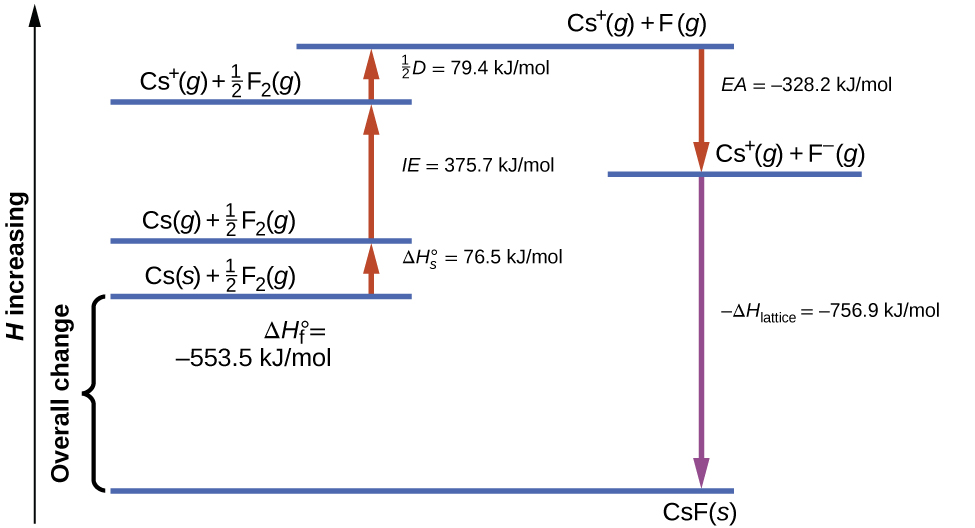
A diagram is shown. An upward facing arrow is drawn to the far left of the chart and is labeled “H increasing.” A horizontal line is drawn at the bottom of the chart. A downward-facing, vertical arrow to the left side of this line is labeled, “Overall change.” Beside this arrow is another label, “capital delta H subscript f, equals negative 553.5 k J per mol, ( Enthalpy of formation ).” Three horizontal lines, one above the other, and all above the bottom line, are labeled, from bottom to top, as: “C s ( s ), plus sign, one half F subscript 2, ( g ),” “C s ( g ), plus sign, one half F subscript 2, ( g ),” and “C s, superscript positive sign, ( g ), plus sign, one half F subscript 2, ( g ).” Each of these lines is connected by an upward-facing vertical arrow. Each arrow is labeled, “capital delta H subscript 1, equals 76.5 k J per mol, ( Enthalpy of sublimation ),” “capital delta H subscript 2, equals 375.7 k J per mol, ( ionization energy ),” and “capital delta H subscript 3 equals 79.4 k J / mol ( one half dissociation energy ).” Another horizontal line is drawn in the center top portion of the diagram and is labeled “C s, superscript positive sign, ( g ), plus sign, F, ( g ).” There is one more horizontal line drawn to the right of the overall diagram and located halfway down the image. An arrow connects the top line to this line and is labeled, “capital delta H equals negative 328.2 k J / mol ( electron affinity ).” The line is labeled, “C s superscript positive sign ( g ) plus F superscript negative sign ( g ).” The arrow connecting this line to the bottom line is labeled, “negative capital delta H subscript lattice equals negative 756.9 k J / mol.” The arrow points to a label on the bottom line which reads, “C s F ( s ).”
The Born-Haber cycle shows the relative energies of each step involved in the formation of an ionic solid from the necessary elements in their reference states.

We begin with the elements in their most common states, Cs( s ) and F 2 ( g ). The Δ H s ° represents the conversion of solid cesium into a gas, and then the ionization energy converts the gaseous cesium atoms into cations. In the next step, we account for the energy required to break the F–F bond to produce fluorine atoms. Converting one mole of fluorine atoms into fluoride ions is an exothermic process, so this step gives off energy (the electron affinity) and is shown as decreasing along the y -axis. We now have one mole of Cs cations and one mole of F anions. These ions combine to produce solid cesium fluoride. The enthalpy change in this step is the negative of the lattice energy, so it is also an exothermic quantity. The total energy involved in this conversion is equal to the experimentally determined enthalpy of formation, Δ H f ° , of the compound from its elements. In this case, the overall change is exothermic.

Hess’s law can also be used to show the relationship between the enthalpies of the individual steps and the enthalpy of formation. [link] shows this for cesium chloride, CsCl 2 .

Enthalpy of sublimation of Cs( s ) Cs ( s ) ⟶ Cs ( g ) Δ H = Δ H s ° = 76.5 kJ
One-half of the bond energy of Cl 2 1 2 Cl 2 ( g ) ⟶ Cl ( g ) Δ H = 1 2 D = 122 kJ
Ionization energy of Na( g ) Na ( g ) ⟶ Na + ( g ) + e − Δ H = I E = 496 kJ
Negative of the electron affinity of Cl Cl ( g ) + e − ⟶ Cl − ( g ) Δ H = − E A = −368 kJ
Negative of the lattice energy of NaCl( s ) Na + ( g ) + Cl − ( g ) ⟶ NaCl ( s ) Δ H = −Δ H lattice = ?
Enthalpy of formation of NaCl( s ), add steps 1–5 Δ H = Δ H f ° = Δ H s ° + 1 2 D + I E + ( − E A ) + ( − Δ H lattice ) Na ( s ) + 1 2 Cl 2 ( g ) ⟶ NaCl ( s ) = −411 kJ

Thus, the lattice energy can be calculated from other values. For cesium chloride, using this data, the lattice energy is:

Δ H lattice = ( 411 + 109 + 122 + 496 + 368 ) kJ = 770 kJ

The Born-Haber cycle may also be used to calculate any one of the other quantities in the equation for lattice energy, provided that the remainder is known. For example, if the relevant enthalpy of sublimation Δ H s ° , ionization energy (IE), bond dissociation enthalpy (D), lattice energy Δ H lattice, and standard enthalpy of formation Δ H f ° are known, the Born-Haber cycle can be used to determine the electron affinity of an atom.

Lattice energies calculated for ionic compounds are typically much higher than bond dissociation energies measured for covalent bonds. Whereas lattice energies typically fall in the range of 600–4000 kJ/mol (some even higher), covalent bond dissociation energies are typically between 150–400 kJ/mol for single bonds. Keep in mind, however, that these are not directly comparable values. For ionic compounds, lattice energies are associated with many interactions, as cations and anions pack together in an extended lattice. For covalent bonds, the bond dissociation energy is associated with the interaction of just two atoms.
<< Chapter < Page Page > Chapter >>
Practice Key Terms 3

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Chemistry. OpenStax CNX. May 20, 2015 Download for free at http://legacy.cnx.org/content/col11760/1.9
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Chemistry' conversation and receive update notifications?

Ask