6.3 Development of quantum theory  (Page 7/25)

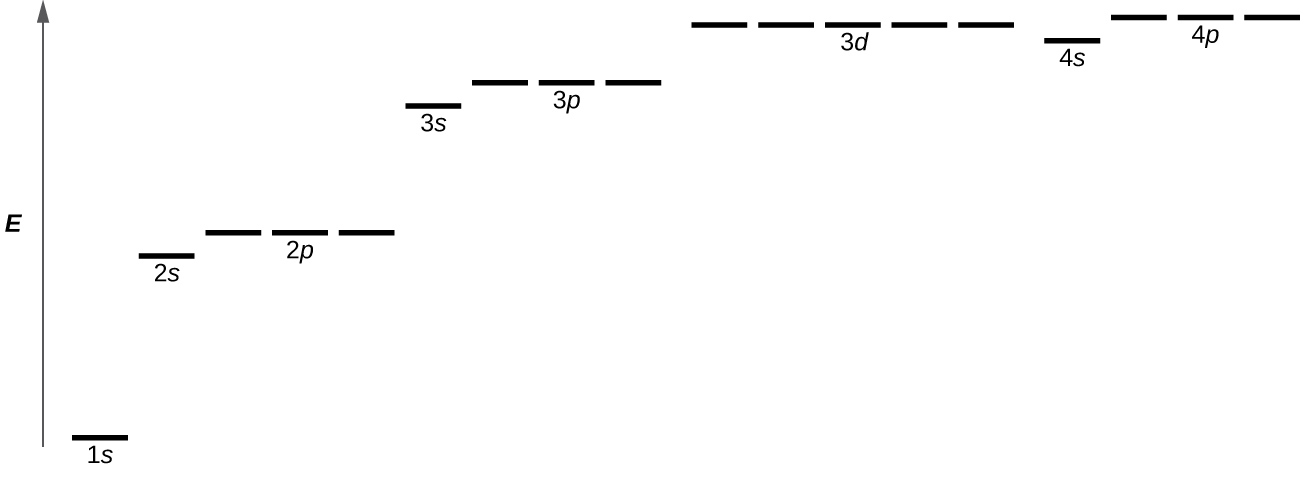
[link] illustrates the energy levels for various orbitals. The number before the orbital name (such as 2 s , 3 p , and so forth) stands for the principle quantum number, n . The letter in the orbital name defines the subshell with a specific angular momentum quantum number l = 0 for s orbitals, 1 for p orbitals, 2 for d orbitals. Finally, there are more than one possible orbitals for l ≥ 1, each corresponding to a specific value of m _l . In the case of a hydrogen atom or a one-electron ion (such as He ⁺ , Li ²⁺ , and so on), energies of all the orbitals with the same n are the same. This is called a degeneracy, and the energy levels for the same principle quantum number, n , are called degenerate energy levels. However, in atoms with more than one electron, this degeneracy is eliminated by the electron–electron interactions, and orbitals that belong to different subshells have different energies, as shown on [link] . Orbitals within the same subshell (for example ns, np, nd, nf , such as 2 p , 3 s ) are still degenerate and have the same energy.

While the three quantum numbers discussed in the previous paragraphs work well for describing electron orbitals, some experiments showed that they were not sufficient to explain all observed results. It was demonstrated in the 1920s that when hydrogen-line spectra are examined at extremely high resolution, some lines are actually not single peaks but, rather, pairs of closely spaced lines. This is the so-called fine structure of the spectrum, and it implies that there are additional small differences in energies of electrons even when they are located in the same orbital. These observations led Samuel Goudsmit and George Uhlenbeck to propose that electrons have a fourth quantum number. They called this the spin quantum number , or m _s .

The other three quantum numbers, n , l , and m _l , are properties of specific atomic orbitals that also define in what part of the space an electron is most likely to be located. Orbitals are a result of solving the Schrödinger equation for electrons in atoms. The electron spin is a different kind of property. It is a completely quantum phenomenon with no analogues in the classical realm. In addition, it cannot be derived from solving the Schrödinger equation and is not related to the normal spatial coordinates (such as the Cartesian x , y , and z ). Electron spin describes an intrinsic electron “rotation” or “spinning.” Each electron acts as a tiny magnet or a tiny rotating object with an angular momentum, even though this rotation cannot be observed in terms of the spatial coordinates.

The magnitude of the overall electron spin can only have one value, and an electron can only “spin” in one of two quantized states. One is termed the α state, with the z component of the spin being in the positive direction of the z axis. This corresponds to the spin quantum number $m_s\text{}=\frac{1}{2}.$ The other is called the β state, with the z component of the spin being negative and $m_s\text{}=-\frac{1}{2}.$ Any electron, regardless of the atomic orbital it is located in, can only have one of those two values of the spin quantum number. The energies of electrons having $m_s\text{}=-\frac{1}{2}$ and $m_s=\frac{1}{2}$ are different if an external magnetic field is applied.