6.3 Development of quantum theory  (Page 2/25)

This is called the de Broglie wavelength . Unlike the other values of λ discussed in this chapter, the de Broglie wavelength is a characteristic of particles and other bodies, not electromagnetic radiation (note that this equation involves velocity [ v , m/s], not frequency [ ν , Hz]. Although these two symbols are identical, they mean very different things). Where Bohr had postulated the electron as being a particle orbiting the nucleus in quantized orbits, de Broglie argued that Bohr’s assumption of quantization can be explained if the electron is considered not as a particle, but rather as a circular standing wave such that only an integer number of wavelengths could fit exactly within the orbit ( [link] ).

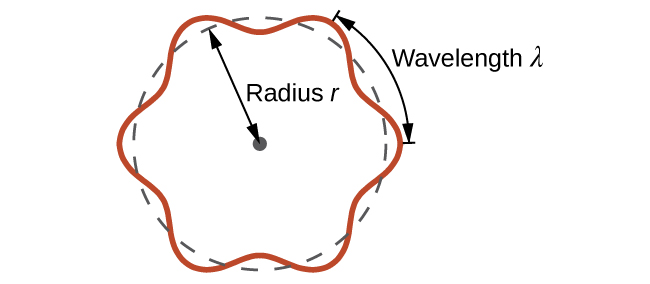
For a circular orbit of radius r , the circumference is 2 πr , and so de Broglie’s condition is:

Since the de Broglie expression relates the wavelength to the momentum and, hence, velocity, this implies:

This expression can be rearranged to give Bohr’s formula for the quantization of the angular momentum:

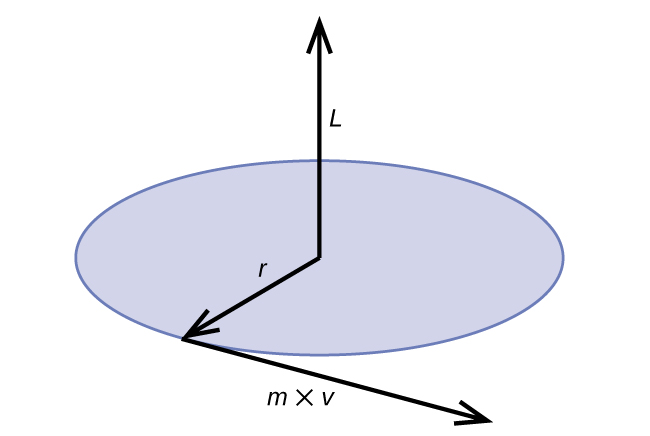
Classical angular momentum L for a circular motion is equal to the product of the radius of the circle and the momentum of the moving particle p .

Shortly after de Broglie proposed the wave nature of matter, two scientists at Bell Laboratories, C. J. Davisson and L. H. Germer , demonstrated experimentally that electrons can exhibit wavelike behavior by showing an interference pattern for electrons travelling through a regular atomic pattern in a crystal. The regularly spaced atomic layers served as slits, as used in other interference experiments. Since the spacing between the layers serving as slits needs to be similar in size to the wavelength of the tested wave for an interference pattern to form, Davisson and Germer used a crystalline nickel target for their “slits,” since the spacing of the atoms within the lattice was approximately the same as the de Broglie wavelengths of the electrons that they used. [link] shows an interference pattern. It is strikingly similar to the interference patterns for light shown in [link] . The wave–particle duality of matter can be seen in [link] by observing what happens if electron collisions are recorded over a long period of time. Initially, when only a few electrons have been recorded, they show clear particle-like behavior, having arrived in small localized packets that appear to be random. As more and more electrons arrived and were recorded, a clear interference pattern that is the hallmark of wavelike behavior emerged. Thus, it appears that while electrons are small localized particles, their motion does not follow the equations of motion implied by classical mechanics, but instead it is governed by some type of a wave equation that governs a probability distribution even for a single electron’s motion. Thus the wave–particle duality first observed with photons is actually a fundamental behavior intrinsic to all quantum particles.