1. Home
  2. Chemistry
  3. Electrochemistry
  4. The nernst equation

17.4 The nernst equation  (Page 8/6)

<< Chapter < Page
  Chemistry     Page 1 / 6
Chapter >> Page >
By the end of this section, you will be able to:
  • Relate cell potentials to free energy changes
  • Use the Nernst equation to determine cell potentials at nonstandard conditions
  • Perform calculations that involve converting between cell potentials, free energy changes, and equilibrium constants

We will now extend electrochemistry by determining the relationship between E cell ° and the thermodynamics quantities such as Δ G ° (Gibbs free energy) and K (the equilibrium constant). In galvanic cells, chemical energy is converted into electrical energy, which can do work. The electrical work is the product of the charge transferred multiplied by the potential difference (voltage):

electrical work = volts × ( charge in coulombs ) = J

The charge on 1 mole of electrons is given by Faraday’s constant ( F )

F = 6.022 × 10 23 e − mol × 1.602 × 10 − 19 C e − = 9.648 × 10 4 C mol = 9.684 × 10 4 J V·mol
total charge = ( number of moles of e − ) × F = n F

In this equation, n is the number of moles of electrons for the balanced oxidation-reduction reaction. The measured cell potential is the maximum potential the cell can produce and is related to the electrical work ( w ele ) by

E cell = − w ele n F or w ele = − n F E cell

The negative sign for the work indicates that the electrical work is done by the system (the galvanic cell) on the surroundings. In an earlier chapter, the free energy was defined as the energy that was available to do work. In particular, the change in free energy was defined in terms of the maximum work ( w max ), which, for electrochemical systems, is w ele .

Δ G = w max = w ele
Δ G = − n F E cell

We can verify the signs are correct when we realize that n and F are positive constants and that galvanic cells, which have positive cell potentials, involve spontaneous reactions. Thus, spontaneous reactions, which have Δ G <0, must have E cell >0. If all the reactants and products are in their standard states, this becomes

Δ G ° = − n F E cell °

This provides a way to relate standard cell potentials to equilibrium constants, since

Δ G ° = − R T ln K
− n F E cell ° = − R T ln K or E cell ° = R T n F ln K

Most of the time, the electrochemical reactions are run at standard temperature (298.15 K). Collecting terms at this temperature yields

E cell ° = R T n F ln K = ( 8.314 J K·mol ) ( 298.15 K ) n × 96,485 C/V·mol ln K = 0.0257 V n ln K

where n is the number of moles of electrons. For historical reasons, the logarithm in equations involving cell potentials is often expressed using base 10 logarithms (log), which changes the constant by a factor of 2.303:

E cell ° = 0.0 592 V n log K

Thus, if Δ G °, K , or E cell ° is known or can be calculated, the other two quantities can be readily determined. The relationships are shown graphically in [link] .

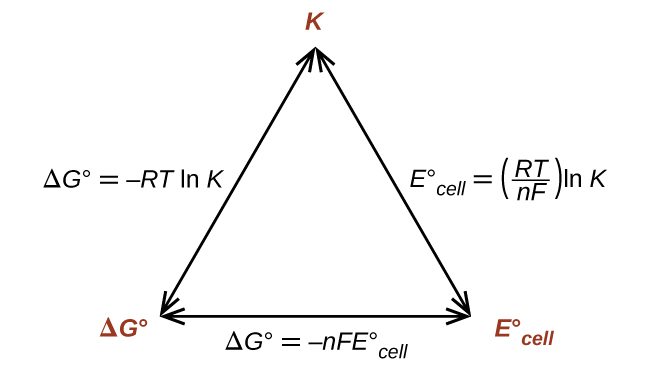
A diagram is shown that involves three double headed arrows positioned in the shape of an equilateral triangle. The vertices are labeled in red. The top vertex is labeled “K.“ The vertex at the lower left is labeled “delta G superscript degree symbol.” The vertex at the lower right is labeled “E superscript degree symbol subscript cell.” The right side of the triangle is labeled “E superscript degree symbol subscript cell equals ( R T divided by n F ) l n K.” The lower side of the triangle is labeled “delta G superscript degree symbol equals negative n F E superscript degree symbol subscript cell.” The left side of the triangle is labeled “delta G superscript degree symbol equals negative R T l n K.”
The relationships between Δ G °, K , and E cell ° . Given any one of the three quantities, the other two can be calculated, so any of the quantities could be used to determine whether a process was spontaneous.

Given any one of the quantities, the other two can be calculated.

Equilibrium constants, standard cell potentials, and standard free energy changes

What is the standard free energy change and equilibrium constant for the following reaction at 25 °C?

2 Ag + ( a q ) + Fe ( s ) ⇌ 2Ag ( s ) + Fe 2+ ( a q )

Solution

The reaction involves an oxidation-reduction reaction, so the standard cell potential can be calculated using the data in Appendix L .

anode (oxidation): Fe ( s ) ⟶ Fe 2+ ( a q ) + 2e − E Fe 2+ /Fe ° = −0.447 V cathode (reduction): 2 × ( Ag + ( a q ) + e − ⟶ Ag ( s ) ) E Ag + /Ag ° = 0.7996 V E cell ° = E cathode ° − E anode ° = E Ag + /Ag ° − E Fe 2+ /Fe ° = +1.247 V

Remember that the cell potential for the cathode is not multiplied by two when determining the standard cell potential. With n = 2, the equilibrium constant is then

E cell ° = 0.0592 V n log K
K = 10 n × E cell ° / 0.0592 V
K = 10 2 × 1.247 V/0.0592 V
K = 10 42.128
K = 1.3 × 10 42

The two equilibrium constants differ slightly due to rounding in the constants 0.0257 V and 0.0592 V. The standard free energy is then

Δ G ° = − n F E cell °
Δ G ° = −2 × 96,485 J V·mol × 1.247 V = −240.6 kJ mol

Check your answer: A positive standard cell potential means a spontaneous reaction, so the standard free energy change should be negative, and an equilibrium constant should be>1.

Check your learning

What is the standard free energy change and the equilibrium constant for the following reaction at room temperature? Is the reaction spontaneous?

Sn ( s ) + 2 Cu 2+ ( a q ) ⇌ Sn 2+ ( a q ) + 2 Cu + ( a q )

Answer:

Spontaneous; n = 2; E cell ° = +0.291 V ; Δ G ° = −56.2 kJ mol ; K = 6.8 × 10 9 .

Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>
Practice Key Terms 4

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Chemistry. OpenStax CNX. May 20, 2015 Download for free at http://legacy.cnx.org/content/col11760/1.9
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Chemistry' conversation and receive update notifications?

Ask