| << Chapter < Page | Chapter >> Page > |
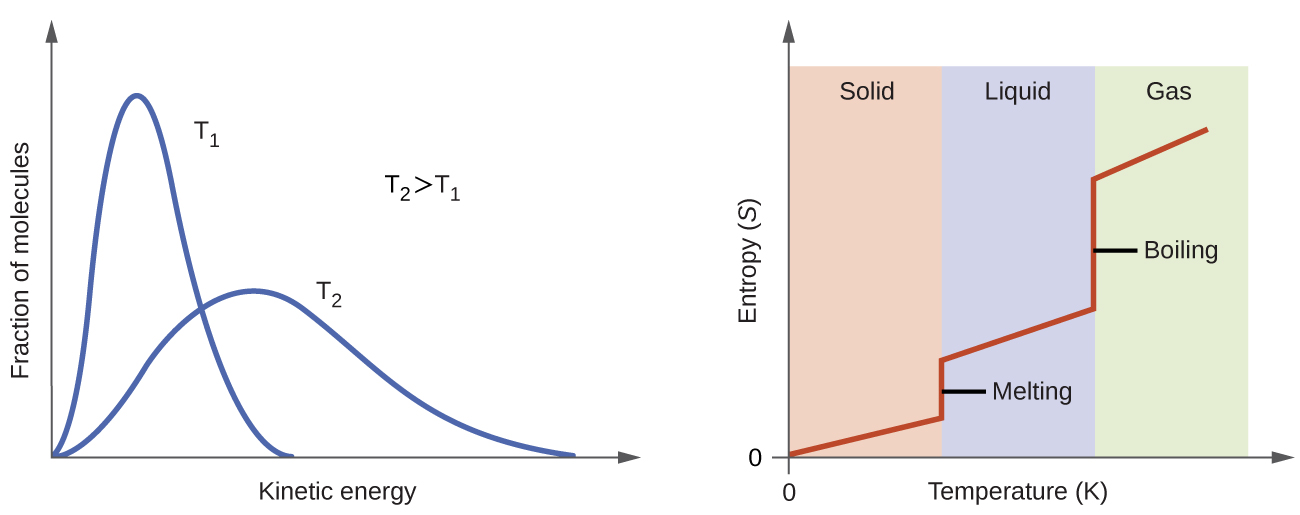
According to kinetic-molecular theory, the temperature of a substance is proportional to the average kinetic energy of its particles. Raising the temperature of a substance will result in more extensive vibrations of the particles in solids and more rapid translations of the particles in liquids and gases. At higher temperatures, the distribution of kinetic energies among the atoms or molecules of the substance is also broader (more dispersed) than at lower temperatures. Thus, the entropy for any substance increases with temperature ( [link] ).
Try this simulator with interactive visualization of the dependence of particle location and freedom of motion on physical state and temperature.
The entropy of a substance is influenced by structure of the particles (atoms or molecules) that comprise the substance. With regard to atomic substances, heavier atoms possess greater entropy at a given temperature than lighter atoms, which is a consequence of the relation between a particle’s mass and the spacing of quantized translational energy levels (which is a topic beyond the scope of our treatment). For molecules, greater numbers of atoms (regardless of their masses) increase the ways in which the molecules can vibrate and thus the number of possible microstates and the system entropy.
Finally, variations in the types of particles affects the entropy of a system. Compared to a pure substance, in which all particles are identical, the entropy of a mixture of two or more different particle types is greater. This is because of the additional orientations and interactions that are possible in a system comprised of nonidentical components. For example, when a solid dissolves in a liquid, the particles of the solid experience both a greater freedom of motion and additional interactions with the solvent particles. This corresponds to a more uniform dispersal of matter and energy and a greater number of microstates. The process of dissolution therefore involves an increase in entropy, Δ S >0.
Considering the various factors that affect entropy allows us to make informed predictions of the sign of Δ S for various chemical and physical processes as illustrated in [link] .
(a) One mole liquid water at room temperature one mole liquid water at 50 °C
(b)
(c)
(d)
(b) negative, reduction in the number of ions (particles) in solution, decreased dispersal of matter
(c) negative, net decrease in the amount of gaseous species
(d) positive, phase transition from solid to liquid, net increase in dispersal of matter
(a)
(b) the freezing of liquid water
(c)
(d)
(a) Positive; The solid dissolves to give an increase of mobile ions in solution. (b) Negative; The liquid becomes a more ordered solid. (c) Positive; The relatively ordered solid becomes a gas. (d) Positive; There is a net production of one mole of gas.

Notification Switch
Would you like to follow the 'Chemistry' conversation and receive update notifications?