10.6 Lattice structures in crystalline solids  (Page 2/29)

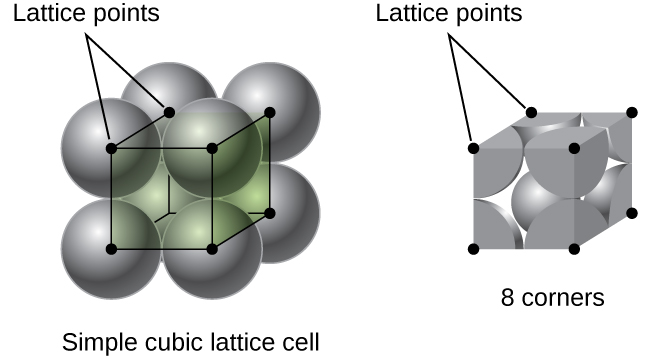
In a simple cubic lattice, the unit cell that repeats in all directions is a cube defined by the centers of eight atoms, as shown in [link] . Atoms at adjacent corners of this unit cell contact each other, so the edge length of this cell is equal to two atomic radii, or one atomic diameter. A cubic unit cell contains only the parts of these atoms that are within it. Since an atom at a corner of a simple cubic unit cell is contained by a total of eight unit cells, only one-eighth of that atom is within a specific unit cell. And since each simple cubic unit cell has one atom at each of its eight “corners,” there is $8\times \frac{1}{8}=1$ atom within one simple cubic unit cell.

Calculation of atomic radius and density for metals, part 1

The edge length of the unit cell of alpha polonium is 336 pm.

(a) Determine the radius of a polonium atom.

(b) Determine the density of alpha polonium.

Solution

Alpha polonium crystallizes in a simple cubic unit cell:

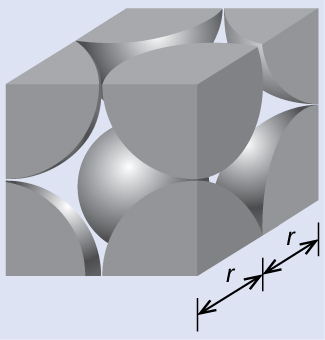
(a) Two adjacent Po atoms contact each other, so the edge length of this cell is equal to two Po atomic radii: l = 2 r . Therefore, the radius of Po is $r=\frac{\text{l}}{2}=\frac{\text{336 pm}}{2}=\text{168 pm}.$

(b) Density is given by $\text{density}=\frac{\text{mass}}{\text{volume}}.$ The density of polonium can be found by determining the density of its unit cell (the mass contained within a unit cell divided by the volume of the unit cell). Since a Po unit cell contains one-eighth of a Po atom at each of its eight corners, a unit cell contains one Po atom.

The mass of a Po unit cell can be found by:

$\text{1 Po unit cell}\times \frac{\text{1 Po atom}}{\text{1 Po unit cell}}\times \frac{\text{1 mol Po}}{6.022\times {10}^{23}\text{Po atoms}}\times \frac{208.998\text{g}}{\text{1 mol Po}}=3.47\times {10}^{\mathrm{-22}}\text{g}$

The volume of a Po unit cell can be found by:

$V=l^3={\left(336\times {10}^{\mathrm{-10}}\text{cm}\right)}^3=3.79\times {10}^{\mathrm{-23}}{\text{cm}}^3$

(Note that the edge length was converted from pm to cm to get the usual volume units for density.)

Therefore, the density of $\text{Po}=\frac{3.471\times {10}^{\mathrm{-22}}\text{g}}{3.79\times {10}^{\mathrm{-23}}{\text{cm}}^3}={\text{9.16 g/cm}}^3$

Check your learning

The edge length of the unit cell for nickel is 0.3524 nm. The density of Ni is 8.90 g/cm ³ . Does nickel crystallize in a simple cubic structure? Explain.

Answer:

No. If Ni was simple cubic, its density would be given by:
$\text{1 Ni atom}\times \frac{\text{1 mol Ni}}{6.022\times {10}^{23}\text{Ni atoms}}\times \frac{58.693\text{g}}{\text{1 mol Ni}}=9.746\times {10}^{\mathrm{-23}}\text{g}$
$V=l^3={\left(3.524\times {10}^{\mathrm{-8}}\text{cm}\right)}^3=4.376\times {10}^{\mathrm{-23}}{\text{cm}}^3$
Then the density of Ni would be $=\frac{9.746\times {10}^{\mathrm{-23}}\text{g}}{4.376\times {10}^{\mathrm{-23}}{\text{cm}}^3}={\text{2.23 g/cm}}^3$
Since the actual density of Ni is not close to this, Ni does not form a simple cubic structure.

Got questions? Get instant answers now!

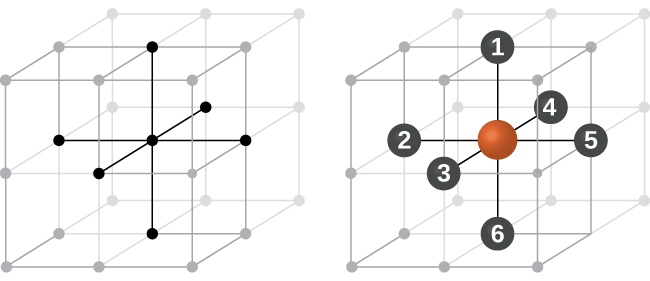
Most metal crystals are one of the four major types of unit cells. For now, we will focus on the three cubic unit cells: simple cubic (which we have already seen), body-centered cubic unit cell    , and face-centered cubic unit cell    —all of which are illustrated in [link] . (Note that there are actually seven different lattice systems, some of which have more than one type of lattice, for a total of 14 different types of unit cells. We leave the more complicated geometries for later in this module.)