| << Chapter < Page | Chapter >> Page > |
We have shown how to use the first and second derivatives of a function to describe the shape of a graph. To graph a function defined on an unbounded domain, we also need to know the behavior of as In this section, we define limits at infinity and show how these limits affect the graph of a function. At the end of this section, we outline a strategy for graphing an arbitrary function
We begin by examining what it means for a function to have a finite limit at infinity. Then we study the idea of a function with an infinite limit at infinity. Back in Introduction to Functions and Graphs , we looked at vertical asymptotes; in this section we deal with horizontal and oblique asymptotes.
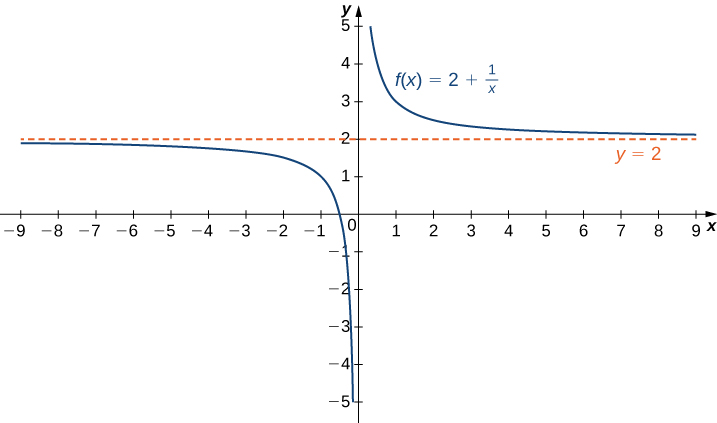
Recall that means becomes arbitrarily close to as long as is sufficiently close to We can extend this idea to limits at infinity. For example, consider the function As can be seen graphically in [link] and numerically in [link] , as the values of get larger, the values of approach We say the limit as approaches of is and write Similarly, for as the values get larger, the values of approaches We say the limit as approaches of is and write
More generally, for any function we say the limit as of is if becomes arbitrarily close to as long as is sufficiently large. In that case, we write Similarly, we say the limit as of is if becomes arbitrarily close to as long as and is sufficiently large. In that case, we write We now look at the definition of a function having a limit at infinity.
(Informal) If the values of become arbitrarily close to as becomes sufficiently large, we say the function has a limit at infinity and write
If the values of becomes arbitrarily close to for as becomes sufficiently large, we say that the function has a limit at negative infinity and write
If the values are getting arbitrarily close to some finite value as or the graph of approaches the line In that case, the line is a horizontal asymptote of ( [link] ). For example, for the function since the line is a horizontal asymptote of
If or we say the line is a horizontal asymptote of
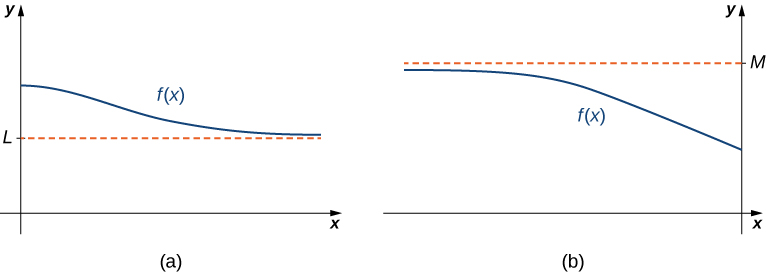

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?