| << Chapter < Page | Chapter >> Page > |
We have just seen how derivatives allow us to compare related quantities that are changing over time. In this section, we examine another application of derivatives: the ability to approximate functions locally by linear functions. Linear functions are the easiest functions with which to work, so they provide a useful tool for approximating function values. In addition, the ideas presented in this section are generalized later in the text when we study how to approximate functions by higher-degree polynomials Introduction to Power Series and Functions .
Consider a function that is differentiable at a point Recall that the tangent line to the graph of at is given by the equation
For example, consider the function at Since is differentiable at and we see that Therefore, the tangent line to the graph of at is given by the equation
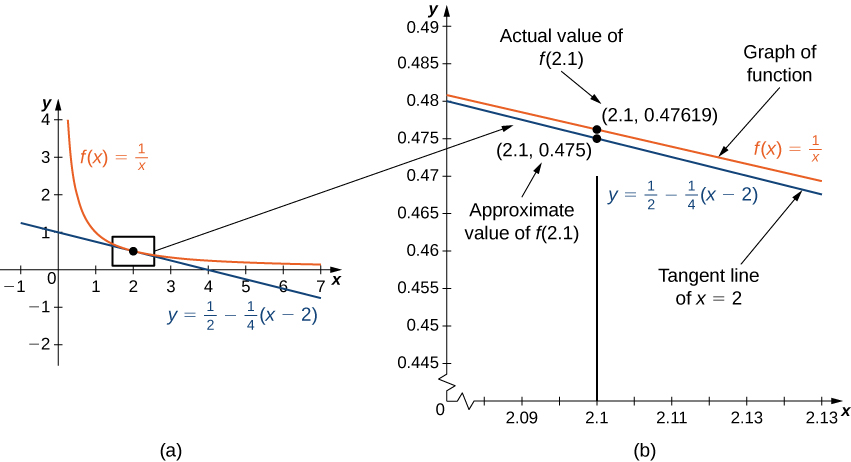
[link] (a) shows a graph of along with the tangent line to at Note that for near 2, the graph of the tangent line is close to the graph of As a result, we can use the equation of the tangent line to approximate for near 2. For example, if the value of the corresponding point on the tangent line is
The actual value of is given by
Therefore, the tangent line gives us a fairly good approximation of ( [link] (b)). However, note that for values of far from 2, the equation of the tangent line does not give us a good approximation. For example, if the -value of the corresponding point on the tangent line is
whereas the value of the function at is
In general, for a differentiable function the equation of the tangent line to at can be used to approximate for near Therefore, we can write
We call the linear function
the linear approximation , or tangent line approximation , of at This function is also known as the linearization of at
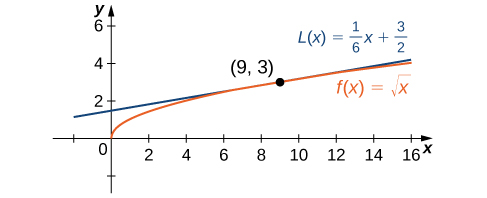
To show how useful the linear approximation can be, we look at how to find the linear approximation for at
Find the linear approximation of at and use the approximation to estimate
Since we are looking for the linear approximation at using [link] we know the linear approximation is given by
We need to find and
Therefore, the linear approximation is given by [link] .
Using the linear approximation, we can estimate by writing

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?