4.10 Antiderivatives  (Page 2/10)

We use this fact and our knowledge of derivatives to find all the antiderivatives for several functions.

Indefinite integrals

We now look at the formal notation used to represent antiderivatives and examine some of their properties. These properties allow us to find antiderivatives of more complicated functions. Given a function $f,$ we use the notation $f^{\prime }\left(x\right)$ or $\frac{df}{dx}$ to denote the derivative of $f.$ Here we introduce notation for antiderivatives. If $F$ is an antiderivative of $f,$ we say that $F\left(x\right)+C$ is the most general antiderivative of $f$ and write

The symbol ${\displaystyle \int }$ is called an integral sign , and ${\displaystyle \int f\left(x\right)dx}$ is called the indefinite integral of $f.$

Given the terminology introduced in this definition, the act of finding the antiderivatives of a function $f$ is usually referred to as integrating $f.$

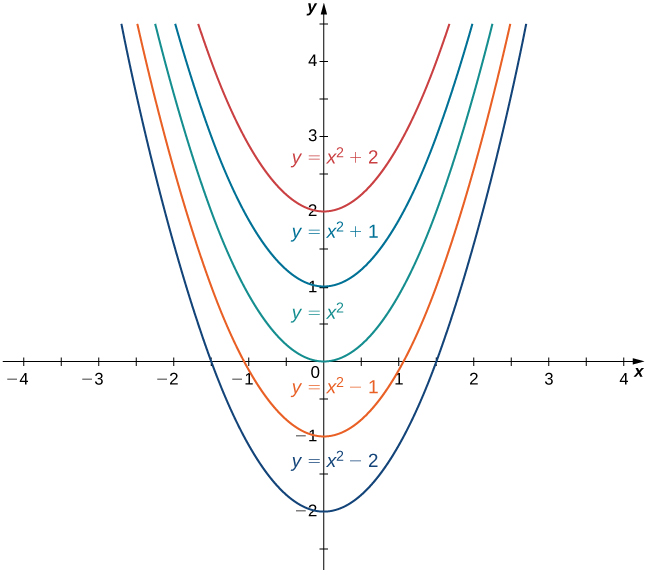
For a function $f$ and an antiderivative $F,$ the functions $F\left(x\right)+C,$ where $C$ is any real number, is often referred to as the family of antiderivatives of $f.$ For example, since $x^2$ is an antiderivative of $2x$ and any antiderivative of $2x$ is of the form $x^2+C,$ we write

The collection of all functions of the form $x^2+C,$ where $C$ is any real number, is known as the family of antiderivatives of $2x.$ [link] shows a graph of this family of antiderivatives.

For some functions, evaluating indefinite integrals follows directly from properties of derivatives. For example, for $n\ne \text{−}1,$

which comes directly from

This fact is known as the power rule for integrals .

Evaluating indefinite integrals for some other functions is also a straightforward calculation. The following table lists the indefinite integrals for several common functions. A more complete list appears in Appendix B .