4.1 Related rates  (Page 2/7)

Step 1. Draw a picture, introducing variables to represent the different quantities involved.

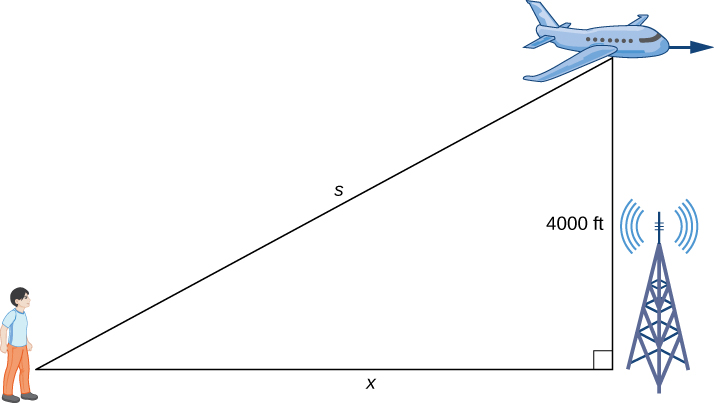
As shown, $x$ denotes the distance between the man and the position on the ground directly below the airplane. The variable $s$ denotes the distance between the man and the plane. Note that both $x$ and $s$ are functions of time. We do not introduce a variable for the height of the plane because it remains at a constant elevation of $4000\text{ft}.$ Since an object’s height above the ground is measured as the shortest distance between the object and the ground, the line segment of length 4000 ft is perpendicular to the line segment of length $x$ feet, creating a right triangle.

Step 2. Since $x$ denotes the horizontal distance between the man and the point on the ground below the plane, $dx\text{/}dt$ represents the speed of the plane. We are told the speed of the plane is 600 ft/sec. Therefore, $\frac{dx}{dt}=600$ ft/sec. Since we are asked to find the rate of change in the distance between the man and the plane when the plane is directly above the radio tower, we need to find $ds\text{/}dt$ when $x=3000\text{ft}.$

Step 3. From the figure, we can use the Pythagorean theorem to write an equation relating $x$ and $s\text{:}$

Step 4. Differentiating this equation with respect to time and using the fact that the derivative of a constant is zero, we arrive at the equation

Step 5. Find the rate at which the distance between the man and the plane is increasing when the plane is directly over the radio tower. That is, find $\frac{ds}{dt}$ when $x=3000\text{ft}.$ Since the speed of the plane is $600\text{ft/sec},$ we know that $\frac{dx}{dt}=600\text{ft/sec}.$ We are not given an explicit value for $s;$ however, since we are trying to find $\frac{ds}{dt}$ when $x=3000\text{ft},$ we can use the Pythagorean theorem to determine the distance $s$ when $x=3000$ and the height is $4000\text{ft}.$ Solving the equation

for $s,$ we have $s=5000\text{ft}$ at the time of interest. Using these values, we conclude that $ds\text{/}dt$ is a solution of the equation

Therefore,

Note : When solving related-rates problems, it is important not to substitute values for the variables too soon. For example, in step 3, we related the variable quantities $x\left(t\right)$ and $s\left(t\right)$ by the equation

Since the plane remains at a constant height, it is not necessary to introduce a variable for the height, and we are allowed to use the constant 4000 to denote that quantity. However, the other two quantities are changing. If we mistakenly substituted $x(t)=3000$ into the equation before differentiating, our equation would have been

After differentiating, our equation would become

As a result, we would incorrectly conclude that $\frac{ds}{dt}=0.$