26.5 The expanding universe  (Page 6/27)

The ant at 4 centimeters, originally 2 centimeters away from our ant, has doubled its distance in 1 minute; it therefore moved away at a speed of 2 centimeters per minute. The ant at the 7-centimeters mark, which was originally 5 centimeters away from our ant, is now 10 centimeters away; it thus had to move at 5 centimeters per minute. The one that started at the 12-centimeters mark, which was 10 centimeters away from the ant doing the counting, is now 20 centimeters away, meaning it must have raced away at a speed of 10 centimeters per minute. Ants at different distances move away at different speeds, and their speeds are proportional to their distances (just as Hubble’s law indicates for galaxies). Yet, notice in our example that all the ruler was doing was stretching uniformly. Also, notice that none of the ants were actually moving of their own accord, it was the stretching of the ruler that moved them apart.

Now let’s repeat the analysis, but put the intelligent ant on some other mark—say, on 7 or 12 centimeters. We discover that, as long as the ruler stretches uniformly, this ant also finds every other ant moving away at a speed proportional to its distance. In other words, the kind of relationship expressed by Hubble’s law can be explained by a uniform stretching of the “world” of the ants. And all the ants in our simple diagram will see the other ants moving away from them as the ruler stretches.

For a three-dimensional analogy, let’s look at the loaf of raisin bread in [link] . The chef has accidentally put too much yeast in the dough, and when she sets the bread out to rise, it doubles in size during the next hour, causing all the raisins to move farther apart. On the figure, we again pick a representative raisin (that is not at the edge or the center of the loaf) and show the distances from it to several others in the figure (before and after the loaf expands).

Expanding raisin bread.

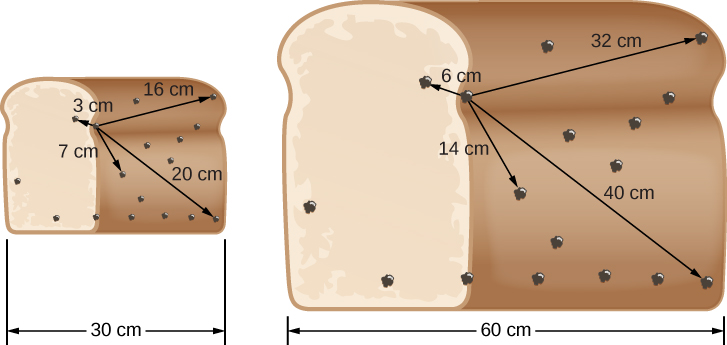
Measure the increases in distance and calculate the speeds for yourself on the raisin bread, just like we did for the ruler. You will see that, since each distance doubles during the hour, each raisin moves away from our selected raisin at a speed proportional to its distance. The same is true no matter which raisin you start with.

Our two analogies are useful for clarifying our thinking, but you must not take them literally. On both the ruler and the raisin bread, there are points that are at the end or edge. You can use these to pinpoint the middle of the ruler and the loaf. While our models of the universe have some resemblance to the properties of the ruler and the loaf, the universe has no boundaries, no edges, and no center (all mind-boggling ideas that we will discuss in a later chapter).

What is useful to notice about both the ants and the raisins is that they themselves did not “cause” their motion. It isn’t as if the raisins decided to take a trip away from each other and then hopped on a hoverboard to get away. No, in both our analogies, it was the stretching of the medium (the ruler or the bread) that moved the ants or the raisins farther apart. In the same way, we will see in The Big Bang chapter that the galaxies don’t have rocket motors propelling them away from each other. Instead, they are passive participants in the expansion of space . As space stretches, the galaxies are carried farther and farther apart much as the ants and the raisins were. (If this notion of the “stretching” of space surprises or bothers you, now would be a good time to review the information about spacetime in Black Holes and Curved Spacetime . We will discuss these ideas further as our discussion broadens from galaxies to the whole universe.)