| << Chapter < Page | Chapter >> Page > |
Unlike a book or your roommate, stars produce measurable distortions in spacetime. A white dwarf, with its stronger surface gravity, produces more distortion just above its surface than does a red giant with the same mass. So, you see, we are eventually going to talk about collapsing stars again, but not before discussing Einstein’s ideas (and the evidence for them) in more detail.
How can we understand the distortion of spacetime by the presence of some (significant) amount of mass? Let’s try the following analogy. You may have seen maps of New York City that squeeze the full three dimensions of this towering metropolis onto a flat sheet of paper and still have enough information so tourists will not get lost. Let’s do something similar with diagrams of spacetime.
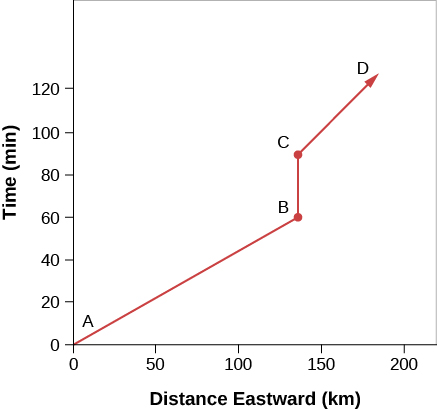
[link] , for example, shows the progress of a motorist driving east on a stretch of road in Kansas where the countryside is absolutely flat. Since our motorist is traveling only in the east-west direction and the terrain is flat, we can ignore the other two dimensions of space. The amount of time elapsed since he left home is shown on the y -axis, and the distance traveled eastward is shown on the x -axis. From A to B he drove at a uniform speed; unfortunately, it was too fast a uniform speed and a police car spotted him. From B to C he stopped to receive his ticket and made no progress through space, only through time. From C to D he drove more slowly because the police car was behind him.
Now let’s try illustrating the distortions of spacetime in two dimensions. In this case, we will (in our imaginations) use a rubber sheet that can stretch or warp if we put objects on it.
Let’s imagine stretching our rubber sheet taut on four posts. To complete the analogy, we need something that normally travels in a straight line (as light does). Suppose we have an extremely intelligent ant—a friend of the comic book superhero Ant-Man, perhaps—that has been trained to walk in a straight line.
We begin with just the rubber sheet and the ant, simulating empty space with no mass in it. We put the ant on one side of the sheet and it walks in a beautiful straight line over to the other side ( [link] ). We next put a small grain of sand on the rubber sheet. The sand does distort the sheet a tiny bit, but this is not a distortion that we or the ant can measure. If we send the ant so it goes close to, but not on top of, the sand grain, it has little trouble continuing to walk in a straight line.
Now we grab something with a little more mass—say, a small pebble. It bends or distorts the sheet just a bit around its position. If we send the ant into this region, it finds its path slightly altered by the distortion of the sheet. The distortion is not large, but if we follow the ant’s path carefully, we notice it deviating slightly from a straight line.
The effect gets more noticeable as we increase the mass of the object that we put on the sheet. Let’s say we now use a massive paperweight. Such a heavy object distorts or warps the rubber sheet very effectively, putting a good sag in it. From our point of view, we can see that the sheet near the paperweight is no longer straight.
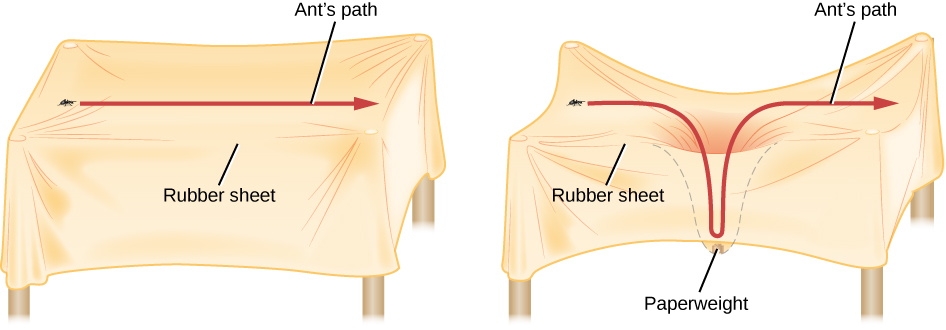
Now let’s again send the ant on a journey that takes it close to, but not on top of, the paperweight. Far away from the paperweight, the ant has no trouble doing its walk, which looks straight to us. As it nears the paperweight, however, the ant is forced down into the sag. It must then climb up the other side before it can return to walking on an undistorted part of the sheet. All this while, the ant is following the shortest path it can, but through no fault of its own (after all, ants can’t fly, so it has to stay on the sheet) this path is curved by the distortion of the sheet itself.
In the same way, according to Einstein’s theory, light always follows the shortest path through spacetime. But the mass associated with large concentrations of matter distorts spacetime, and the shortest, most direct paths are no longer straight lines, but curves.
How large does a mass have to be before we can measure a change in the path followed by light? In 1916, when Einstein first proposed his theory, no distortion had been detected at the surface of Earth (so Earth might have played the role of the grain of sand in our analogy). Something with a mass like our Sun’s was necessary to detect the effect Einstein was describing (we will discuss how this effect was measured using the Sun in the next section).
The paperweight in our analogy might be a white dwarf or a neutron star. The distortion of spacetime is greater near the surfaces of these compact, massive objects than near the surface of the Sun. And when, to return to the situation described at the beginning of the chapter, a star core with more than three times the mass of the Sun collapses forever, the distortions of spacetime very close to it can become truly mind-boggling.
By considering the consequences of the equivalence principle, Einstein concluded that we live in a curved spacetime. The distribution of matter determines the curvature of spacetime; other objects (and even light) entering a region of spacetime must follow its curvature. Light must change its path near a massive object not because light is bent by gravity, but because spacetime is.

Notification Switch
Would you like to follow the 'Astronomy' conversation and receive update notifications?