| << Chapter < Page | Chapter >> Page > |
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
identity; all real numbers
Classify as a conditional equation, an identity, or a contradiction. Then state the solution.
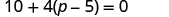 | |
| Distribute. |
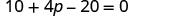 |
| Combine like terms. |
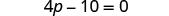 |
| Add to both sides. |
 |
| Simplify. |
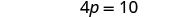 |
| Divide. |
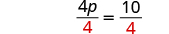 |
| Simplify. |
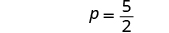 |
| The equation is true when . | This is a conditional equation.
The solution is |
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
conditional equation;
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
conditional equation;
Classify the equation as a conditional equation, an identity, or a contradiction. Then state the solution.
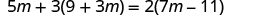 | |
| Distribute. |
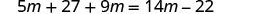 |
| Combine like terms. |
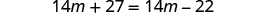 |
| Subtract from both sides. |
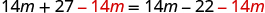 |
| Simplify. |
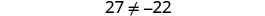 |
| But . | The equation is a contradiction.
It has no solution. |
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
contradiction; no solution
Classify the equation as a conditional equation, an identity, or a contradiction and then state the solution:
contradiction; no solution
| Type of equation | What happens when you solve it? | Solution |
|---|---|---|
| Conditional Equation | True for one or more values of the variables and false for all other values | One or more values |
| Identity | True for any value of the variable | All real numbers |
| Contradiction | False for all values of the variable | No solution |
Solve Equations Using the General Strategy for Solving Linear Equations
In the following exercises, solve each linear equation.
Classify Equations
In the following exercises, classify each equation as a conditional equation, an identity, or a contradiction and then state the solution.
Fencing Micah has 44 feet of fencing to make a dog run in his yard. He wants the length to be 2.5 feet more than the width. Find the length, L , by solving the equation .
Coins Rhonda has $1.90 in nickels and dimes. The number of dimes is one less than twice the number of nickels. Find the number of nickels, n , by solving the equation .
8 nickels
Using your own words, list the steps in the general strategy for solving linear equations.
Explain why you should simplify both sides of an equation as much as possible before collecting the variable terms to one side and the constant terms to the other side.
Answers will vary.
What is the first step you take when solving the equation ? Why is this your first step?
Solve the equation explaining all the steps of your solution as in the examples in this section.
Answers will vary.
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objective of this section.

ⓑ On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?