1. Home
  2. Elementary algebra
  3. Polynomials
  4. Multiply polynomials

6.3 Multiply polynomials  (Page 2/3)

<< Chapter < Page
  Elementary algebra     Page 2 / 3
Chapter >> Page >
( x − 2 ) ( x − y ) x 2 − x y − 2 x + 2 y F O I L

Let’s look at ( x + 3 ) ( x + 7 ) .

Distibutive Property FOIL
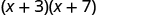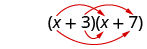The product of x plus 3 and x plus 7. The product of x plus 3 and x plus y. An arrow extends from the x in x plus 3 to the x in x plus 7. A second arrow extends from the x in x plus 3 to the 7 in x plus 7. A third arrow extends from the 3 in x plus 3 to the x in x plus 7. A fourth arrow extends from the 3 in x plus 3 to the 7 in x plus 7.
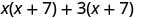The sum of two products, the product of x and x plus 7, and the product of 3 and x plus 7.
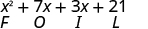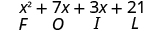x squared plus 7 x plus 3 x plus 21. Below x squared is the letter F, below 7 x is the letter O, below 3 x is the letter I, and below 21 is the letter L, spelling FOIL. x squared plus 7 x plus 3 x plus 21. Below x squared is the letter F, below 7 x is the letter O, below 3 x is the letter I, and below 21 is the letter L, spelling FOIL.
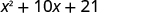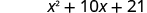x squared plus 10 x plus 21. x squared plus 10 x plus 21.

Notice how the terms in third line fit the FOIL pattern.

Now we will do an example where we use the FOIL pattern to multiply two binomials.

How to multiply a binomial by a binomial using the foil method

Multiply using the FOIL method: ( x + 5 ) ( x + 9 ) .

Solution

This figure is a table that has three columns and five rows. The first column is a header column, and it contains the names and numbers of each step. The second and third columns contain math. On the top row of the table, the first cell on the left reads “Step 1. Multiply the first terms.” The second column contains the product of binomials x plus 5 and x plus 9. Below this is the product of x plus 5 and x plus 9 again, with an arrow extending from the x in the first binomial to the x in the second binomial. The third column contains x squared plus blank plus blank plus blank. Below the x squared is the letter F, and below each of the three blanks are the letters O, I, and L, respectively. In the second row, the first cell reads “Step 2. Multiply the outer terms.” In the second cell is the product of x plus 5 and x plus 9 again, with an arrow extending from x in the first binomial to the 9 in the second binomial. The third cell contains x squared plus 9x plus blank plus blank, with the letter F under the x squared, O under the 9x, and I and L beneath the two blanks. In the third row, the first cell reads “Step 3. Multiply the inner terms.” The second cell contains the product of x plus 5 and x plus 9 again, with an arrow extending from 5 in the first binomial to the x in the second binomial. The third cell contains x squared plus 9x plus 5x plus blank, with F beneath x squared, O beneath 9x, I beneath 5x, and L beneath the blank. In the fourth row, the first cell reads “Step 4. Multiply the last terms.” In the second cell is the product of x plus 5 and x plus 9 again, with an arrow extending from 5 in the first binomial to 9 in the second binomial. The third cell contains x squared plus 9x plus 6x plus 45, with F beneath x squared, O beneath 9x, I beneath 6x, and L beneath 45. In the final row, the first cell reads “Step 5. Combine like terms, when possible.” The second cell is blank. The third cell contains the final expression: x squared plus 15x plus 45.
Got questions? Get instant answers now!
Got questions? Get instant answers now!

Multiply using the FOIL method: ( x + 6 ) ( x + 8 ) .

x 2 + 14 x + 48

Got questions? Get instant answers now!

Multiply using the FOIL method: ( y + 17 ) ( y + 3 ) .

y 2 + 20 y + 51

Got questions? Get instant answers now!

We summarize the steps of the FOIL method below. The FOIL method only applies to multiplying binomials, not other polynomials!

Multiply two binomials using the foil method

.

When you multiply by the FOIL method, drawing the lines will help your brain focus on the pattern and make it easier to apply.

Multiply: ( y − 7 ) ( y + 4 ) .

Solution

This figure has three columns, with written instructions in the first column and math in the second and third columns. At the top of the figure, the text in the first column says “Multiply the first terms.” The second column contains the product of two binomials, y minus 7 and y plus 4, with an arrow extending from the y in the first binomial to the y in the second binomial. The third column contains y squared plus blank plus blank plus blank. Beneath y squared is the letter F and beneath each blank are the letters O, I, and L, respectively. One row down, the text in the first column says “Multiply the outer terms.” The second column contains the product of y minus 7 and y plus 4 again, with a second arrow extending from y in the first binomial to 4 in the second binomial. The third column contains y squared plus 4y plus blank plus blank. Below y squared is F, below 4y is O, and below the blanks are I and L. One row down, the text in the first column says “Multiply the inner terms.” The middle column contains the product of y minus 7 and y plus 4 again, with a third arrow extending from the minus 7 in the first binomial to the y in the second binomial. The third column contains y squared plus 4y minus 7y plus blank. One row down, the text in the first column says “Multiply the last terms.” The second column contains the product of y minus 7 and y plus 4 again, with a fourth arrow extending from minus 7 in the first binomial to 4 in the second binomial. In the third column is the full expression, y squared plus 4y minus 7y minus 28, with each letter of FOIL beneath each of the terms. At the bottom of the image, the text in the first column says “Combine like terms.” In the right column is y squared minus 3y minus 28.

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Multiply: ( x − 7 ) ( x + 5 ) .

x 2 − 2 x − 35

Got questions? Get instant answers now!

Multiply: ( b − 3 ) ( b + 6 ) .

b 2 + 3 b − 18

Got questions? Get instant answers now!

Multiply: ( 4 x + 3 ) ( 2 x − 5 ) .

Solution

This figure has three columns. At the top of the figure, the second column contains the product of two binomials, 4x plus 3 and 2x minus 5. One row down, the text in the first column says “Multiply the first terms. 4x times 2x.” The second column contains 8x squared plus blank plus blank plus blank. Beneath 8x squared is the letter F and beneath each blank are the letters O, I, and L, respectively. One row down, the text in the first column says “Multiply the outer terms. 4x times negative 5.” The second column contains 8x squared minus 20x plus blank plus blank. Below 8x squared is F, below 20x is O, and below the blanks are I and L. One row down, the text in the first column says “Multiply the inner terms. 3 times 2x.” The second column contains 8x squared minus 20x plus 6x plus blank. One row down, the text in the first column says “Multiply the last terms. 3 times negative 5.” The second column contains the full expression, 8x squared minus 20x plus 6x minus 15, with each letter of FOIL beneath each of the terms. At the bottom of the image, the text in the first column says “Combine like terms.” In the right column is 8x squared minus 14x minus 15. In the third column is the product of the two binomials again, 4x plus 3 times 2x minus 5. An arrow extends from 4x in the first binomial to 2x in the second binomial. A second arrow extends from 4x in the first binomial to minus 5 in the second binomial. A third arrow extends from 3 in the first binomial to 2x in the second binomial. A fourth arrow extends from 3 in the first binomial to minus 5 in the second binomial.

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Multiply: ( 3 x + 7 ) ( 5 x − 2 ) .

15 x 2 + 29 x − 14

Got questions? Get instant answers now!

Multiply: ( 4 y + 5 ) ( 4 y − 10 ) .

16 y 2 − 20 y − 50

Got questions? Get instant answers now!

The final products in the last four examples were trinomials because we could combine the two middle terms. This is not always the case.

Multiply: ( 3 x − y ) ( 2 x − 5 ) .

Solution

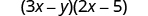The product of two binomials, 3 x minus y and 2 x minus 5.
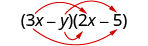An arrow extends from 3 x in the first binomial to 2 x in the second binomial. A second arrow extends from 3 x in the first binomial to minus 5 in the second binomial. A third arrow extends from y in the first binomial to 2 x in the second binomial. A fourth arrow extends from y in the first binomial to minus 5 in the second binomial.
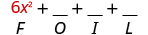Multiply the First . 6 x squared plus blank plus blank plus blank. Beneath 6 x squared is the letter F.
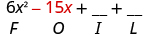Multiply the Outer . 6 x squared minus 15 x plus blank plus blank. Beneath 15 x is the letter O.
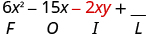Multiply the Inner . 6x squared minus 15x minus 2xy plus blank. Beneath minus 2 x y is the letter I.
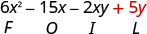Multiply the Last . 6 x squared minus 15 x minus 2 x y plus 5 y. Beneath 5 y is the letter L.
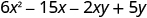Combine like terms—there are none. 6 x squared minus 15 x minus 2 x y plus 5 y.

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Multiply: ( 10 c − d ) ( c − 6 ) .

10 c 2 − 60 c − c d + 6 d

Got questions? Get instant answers now!

Multiply: ( 7 x − y ) ( 2 x − 5 ) .

14 x 2 − 35 x − 2 x y + 10 y

Got questions? Get instant answers now!

Be careful of the exponents in the next example.

Multiply: ( n 2 + 4 ) ( n − 1 ) .

Solution

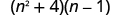The product of two binomials, n squared plus 4 and n minus 1.
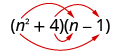The product of two binomials, n squared plus 4 and n minus 1. An arrow extends from n squared in the first binomial to n in the second binomial. A second arrow extends from n squared in the first binomial to minus 1 in the second binomial. A third arrow extends from 4 in the first binomial to n in the second binomial. A fourth arrow extends from 4 in the first binomial to minus 1 in the second binomial.
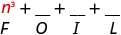Multiply the First . n cubed plus blank plus blank plus blank. Beneath n cubed is the letter F.
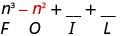Multiply the Outer . n cubed minus n squared plus blank plus blank. Beneath minus n squared is the letter O.
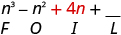Multiply the Inner . n cubed minus n squared plus 4 n plus blank. Beneath 4 n is the letter I.
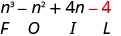Multiply the Last . n cubed minus n squared plus 4 n minus 4. Beneath minus 4 is the letter L.
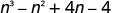Combine like terms—there are none. n cubed minus n squared plus 4 n minus 4.

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Multiply: ( x 2 + 6 ) ( x − 8 ) .

x 3 − 8 x 2 + 6 x − 48

Got questions? Get instant answers now!

Multiply: ( y 2 + 7 ) ( y − 9 ) .

y 3 − 9 y 2 + 7 y − 63

Got questions? Get instant answers now!

Multiply: ( 3 p q + 5 ) ( 6 p q − 11 ) .

Solution

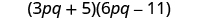The product of two binomials, 3 p q plus 5 and 6 p q minus 11.
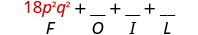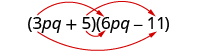Multiply the First . 18 p squared q squared plus blank plus blank plus blank. Beneath 18 p squared q squared is the letter F. The product of two binomials, 3 p q plus 5 and 6 p q minus 11. An arrow extends from 3 p q in the first binomial to 6 p q in the second binomial. A second arrow extends from 3 p q in the first binomial to minus 11 in the second binomial. A third arrow extends from 5 in the first binomial to 6 p q in the second binomial. A fourth arrow extends from 5 in the first binomial to minus 11 in the second binomial.
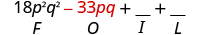Multiply the Outer . 18 p squared q squared minus 33 p q plus blank plus blank. Beneath minus 33 p q is the letter O.
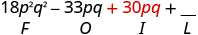Multiply the Inner . 18 p squared q squared minus 33 p q plus 30 p q plus blank. Beneath 30 p q is the letter I.
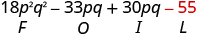Multiply the Last . 18 p squared q squared minus 33 p q plus 30 p q minus 55. Beneath minus 55 is the letter L.
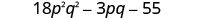Combine like terms—there are none. 18 p squared q squared minus 33 p q plus 30 p q minus 55.

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Multiply: ( 2 a b + 5 ) ( 4 a b − 4 ) .

8 a 2 b 2 + 12 a b − 20

Got questions? Get instant answers now!

Multiply: ( 2 x y + 3 ) ( 4 x y − 5 ) .

8 x 2 y 2 + 2 x y − 15

Got questions? Get instant answers now!

Multiply a binomial by a binomial using the vertical method

The FOIL method is usually the quickest method for multiplying two binomials, but it only works for binomials. You can use the Distributive Property to find the product of any two polynomials. Another method that works for all polynomials is the Vertical Method. It is very much like the method you use to multiply whole numbers. Look carefully at this example of multiplying two-digit numbers.

This figure shows the vertical multiplication of 23 and 46. The number 23 is above the number 46. Below this, there is the partial product 138 over the partial product 92. The final product is at the bottom and is 1058. Text on the right side of the image says “Start by multiplying 23 by 6 to get 138. Next, multiply 23 by 4, lining up the partial product in the correct columns. Last you add the partial products.”

Now we’ll apply this same method to multiply two binomials.

Multiply using the Vertical Method: ( 3 y − 1 ) ( 2 y − 6 ) .

Solution

It does not matter which binomial goes on the top.

Multiply 3 y − 1 by −6 . Multiply 3 y − 1 by 2y. Add like terms. 3 y − 1 × 2 y − 6 ________ −18 y + 6 6 y 2 − 2 y  _____________ 6 y 2 − 20 y + 6 partial product partial product product

Notice the partial products are the same as the terms in the FOIL method.
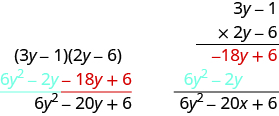
This figure has two columns. In the left column is the product of two binomials, 3y minus 1 and 2y minus 6. Below this is 6y squared minus 2y minus 18y plus 6. Below this is 6y squared minus 20y plus 6. In the right column is the vertical multiplication of 3y minus 1 and 2y minus 6. Below this is the partial product negative 18y plus 6. Below this is the partial product 6y squared minus 2y. Below this is 6y squared minus 20y plus 6.

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Multiply using the Vertical Method: ( 5 m − 7 ) ( 3 m − 6 ) .

15 m 2 − 51 m + 42

Got questions? Get instant answers now!

Multiply using the Vertical Method: ( 6 b − 5 ) ( 7 b − 3 ) .

42 b 2 − 53 b + 15

Got questions? Get instant answers now!

We have now used three methods for multiplying binomials. Be sure to practice each method, and try to decide which one you prefer. The methods are listed here all together, to help you remember them.

Multiplying two binomials

To multiply binomials, use the:

  • Distributive Property
  • FOIL Method
  • Vertical Method

Remember, FOIL only works when multiplying two binomials.

Questions & Answers

A golfer on a fairway is 70 m away from the green, which sits below the level of the fairway by 20 m. If the golfer hits the ball at an angle of 40° with an initial speed of 20 m/s, how close to the green does she come?
Aislinn Reply
cm
tijani
what is titration
John Reply
what is physics
Siyaka Reply
A mouse of mass 200 g falls 100 m down a vertical mine shaft and lands at the bottom with a speed of 8.0 m/s. During its fall, how much work is done on the mouse by air resistance
Jude Reply
Can you compute that for me. Ty
Jude
what is the dimension formula of energy?
David Reply
what is viscosity?
David
what is inorganic
emma Reply
what is chemistry
Youesf Reply
what is inorganic
emma
Chemistry is a branch of science that deals with the study of matter,it composition,it structure and the changes it undergoes
Adjei
please, I'm a physics student and I need help in physics
Adjanou
chemistry could also be understood like the sexual attraction/repulsion of the male and female elements. the reaction varies depending on the energy differences of each given gender. + masculine -female.
Pedro
A ball is thrown straight up.it passes a 2.0m high window 7.50 m off the ground on it path up and takes 1.30 s to go past the window.what was the ball initial velocity
Krampah Reply
2. A sled plus passenger with total mass 50 kg is pulled 20 m across the snow (0.20) at constant velocity by a force directed 25° above the horizontal. Calculate (a) the work of the applied force, (b) the work of friction, and (c) the total work.
Sahid Reply
you have been hired as an espert witness in a court case involving an automobile accident. the accident involved car A of mass 1500kg which crashed into stationary car B of mass 1100kg. the driver of car A applied his brakes 15 m before he skidded and crashed into car B. after the collision, car A s
Samuel Reply
can someone explain to me, an ignorant high school student, why the trend of the graph doesn't follow the fact that the higher frequency a sound wave is, the more power it is, hence, making me think the phons output would follow this general trend?
Joseph Reply
Nevermind i just realied that the graph is the phons output for a person with normal hearing and not just the phons output of the sound waves power, I should read the entire thing next time
Joseph
Follow up question, does anyone know where I can find a graph that accuretly depicts the actual relative "power" output of sound over its frequency instead of just humans hearing
Joseph
"Generation of electrical energy from sound energy | IEEE Conference Publication | IEEE Xplore" ***ieeexplore.ieee.org/document/7150687?reload=true
Ryan
what's motion
Maurice Reply
what are the types of wave
Maurice
answer
Magreth
progressive wave
Magreth
hello friend how are you
Muhammad Reply
fine, how about you?
Mohammed
hi
Mujahid
A string is 3.00 m long with a mass of 5.00 g. The string is held taut with a tension of 500.00 N applied to the string. A pulse is sent down the string. How long does it take the pulse to travel the 3.00 m of the string?
yasuo Reply
Who can show me the full solution in this problem?
Reofrir Reply
Got questions? Join the online conversation and get instant answers!
Jobilize.com Reply
<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Elementary algebra. OpenStax CNX. Jan 18, 2017 Download for free at http://cnx.org/content/col12116/1.2
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Elementary algebra' conversation and receive update notifications?

Ask