5.5 Solve mixture applications with systems of equations  (Page 9/7)

Solve mixture applications

When we solved mixture applications with coins and tickets earlier, we started by creating a table so we could organize the information. For a coin example with nickels and dimes, the table looked like this:

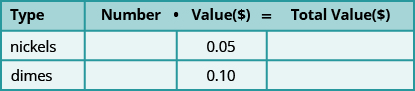
Using one variable meant that we had to relate the number of nickels and the number of dimes. We had to decide if we were going to let n be the number of nickels and then write the number of dimes in terms of n , or if we would let d be the number of dimes and write the number of nickels in terms of d .

Now that we know how to solve systems of equations with two variables, we’ll just let n be the number of nickels and d be the number of dimes. We’ll write one equation based on the total value column, like we did before, and the other equation will come from the number column.

For the first example, we’ll do a ticket problem where the ticket prices are in whole dollars, so we won’t need to use decimals just yet.

Translate to a system of equations and solve:

The box office at a movie theater sold 147 tickets for the evening show, and receipts totaled $1,302. How many $11 adult and how many $8 child tickets were sold?

Solution

Step 1. Read the problem.	We will create a table to organize the information.
Step 2. Identify what we are looking for.	We are looking for the number of adult tickets and the number of child tickets sold.
Step 3. Name what we are looking for.	Let $a=$ the number of adult tickets. $c=$ the number of child tickets
A table will help us organize the data. We have two types of tickets: adult and child.	Write a and c for the number of tickets.
Write the total number of tickets sold at the bottom of the Number column.	Altogether 147 were sold.
Write the value of each type of ticket in the Value column.	The value of each adult ticket is $11. The value of each child tickets is $8.
The number times the value gives the total value, so the total value of adult tickets is $a·11=11a$ , and the total value of child tickets is $c·8=8c.$
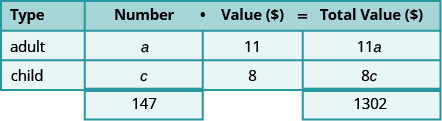Altogether the total value of the tickets was $1,302.	Fill in the Total Value column.
Step 4. Translate into a system of equations.
The Number column and the Total Value column give us the system of equations. We will use the elimination method to solve this system.
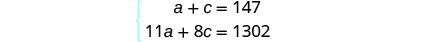Multiply the first equation by −8.
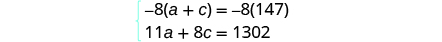Simplify and add, then solve for a .
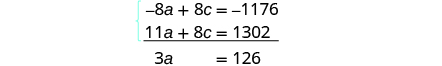Substitute a = 42 into the first equation, then solve for c .
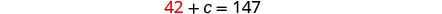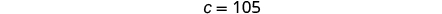Step 5. Check the answer in the problem.   42 adult tickets at $11 per ticket makes $462   105 child tickets at $8 per ticket makes $840.   The total receipts are $1,302.✓
Step 6. Answer the question.	The movie theater sold 42 adult tickets and 105 child tickets.

Got questions? Get instant answers now!

Got questions? Get instant answers now!