2.1 Solve equations using the subtraction and addition properties  (Page 2/6)

What algebraic equation would match this situation? In [link] each side of the workspace represents an expression and the center line takes the place of the equal sign. We will call the contents of the envelope $x$ .

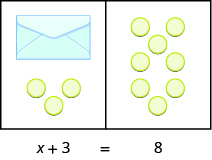
Let’s write algebraically the steps we took to discover how many counters were in the envelope:

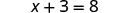First, we took away three from each side.
Then we were left with five.

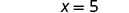Check:

Five in the envelope plus three more does equal eight!

Our model has given us an idea of what we need to do to solve one kind of equation. The goal is to isolate the variable by itself on one side of the equation. To solve equations such as these mathematically, we use the Subtraction Property of Equality .

Let’s see how to use this property to solve an equation. Remember, the goal is to isolate the variable on one side of the equation. And we check our solutions by substituting the value into the equation to make sure we have a true statement.

Solve: $y+37=\mathrm{-13}.$

Solution

To get y by itself, we will undo the addition of 37 by using the Subtraction Property of Equality.

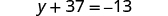Subtract 37 from each side to ‘undo’ the addition.
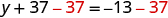Simplify.
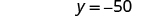Check:
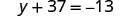Substitute $y=\mathrm{-50}$

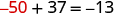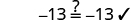Since $y=\mathrm{-50}$ makes $y+37=\mathrm{-13}$ a true statement, we have the solution to this equation.

Got questions? Get instant answers now!

Got questions? Get instant answers now!

What happens when an equation has a number subtracted from the variable, as in the equation $x-5=8$ ? We use another property of equations to solve equations where a number is subtracted from the variable. We want to isolate the variable, so to ‘undo’ the subtraction we will add the number to both sides. We use the Addition Property of Equality .

In [link] , 37 was added to the y and so we subtracted 37 to ‘undo’ the addition. In [link] , we will need to ‘undo’ subtraction by using the Addition Property of Equality .

Solve: $a-28=\mathrm{-37}.$

Solution

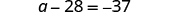Add 28 to each side to ‘undo’ the subtraction.
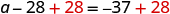Simplify.
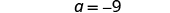Check:
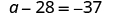Substitute $a=\mathrm{-9}$
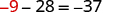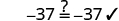	The solution to $a-28=\mathrm{-37}$ is $a=\mathrm{-9}.$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Solve: $x-\frac{5}{8}=\frac{3}{4}.$

Solution

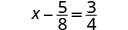Use the Addition Property of Equality.
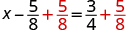Find the LCD to add the fractions on the right.
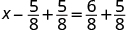Simplify.
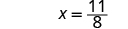Check:
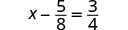Substitute $x=\frac{11}{8}.$
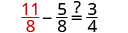Subtract.
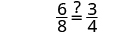Simplify.
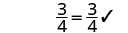	The solution to $x-\frac{5}{8}=\frac{3}{4}$ is $x=\frac{11}{8}.$

Got questions? Get instant answers now!

Got questions? Get instant answers now!

The next example will be an equation with decimals.

Solve: $n-0.63=\mathrm{-4.2}.$

Solution

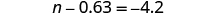Use the Addition Property of Equality.
Add.
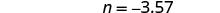Check:
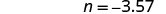Let $n=\mathrm{-3.57}$ .

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Solve equations that require simplification

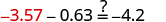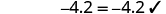In the previous examples, we were able to isolate the variable with just one operation. Most of the equations we encounter in algebra will take more steps to solve. Usually, we will need to simplify one or both sides of an equation before using the Subtraction or Addition Properties of Equality.