| << Chapter < Page | Chapter >> Page > |
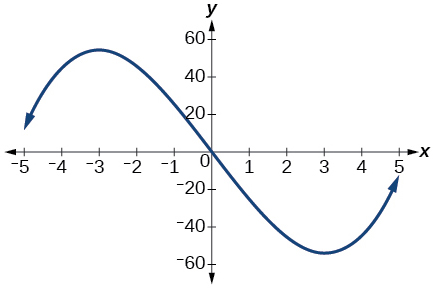
Estimate the intervals where the function is increasing or decreasing.
Estimate the point(s) at which the graph of has a local maximum or a local minimum.
local maximum: local minimum:
For the following exercises, consider the graph in [link] .
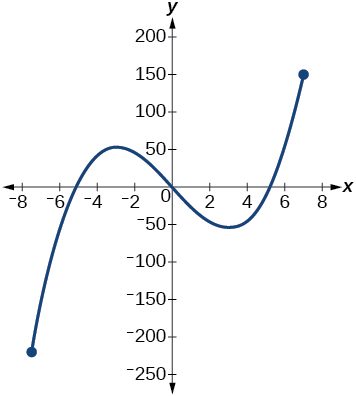
If the complete graph of the function is shown, estimate the intervals where the function is increasing or decreasing.
If the complete graph of the function is shown, estimate the absolute maximum and absolute minimum.
absolute maximum at approximately absolute minimum at approximately
[link] gives the annual sales (in millions of dollars) of a product from 1998 to 2006. What was the average rate of change of annual sales (a) between 2001 and 2002, and (b) between 2001 and 2004?
| Year |
Sales
(millions of dollars) |
|---|---|
| 1998 | 201 |
| 1999 | 219 |
| 2000 | 233 |
| 2001 | 243 |
| 2002 | 249 |
| 2003 | 251 |
| 2004 | 249 |
| 2005 | 243 |
| 2006 | 233 |
[link] gives the population of a town (in thousands) from 2000 to 2008. What was the average rate of change of population (a) between 2002 and 2004, and (b) between 2002 and 2006?
| Year |
Population
(thousands) |
|---|---|
| 2000 | 87 |
| 2001 | 84 |
| 2002 | 83 |
| 2003 | 80 |
| 2004 | 77 |
| 2005 | 76 |
| 2006 | 78 |
| 2007 | 81 |
| 2008 | 85 |
a. –3000; b. –1250
For the following exercises, find the average rate of change of each function on the interval specified.
For the following exercises, use a graphing utility to estimate the local extrema of each function and to estimate the intervals on which the function is increasing and decreasing.
Local maximum at local minima at and decreasing on and increasing on and
The graph of the function is shown in [link] .
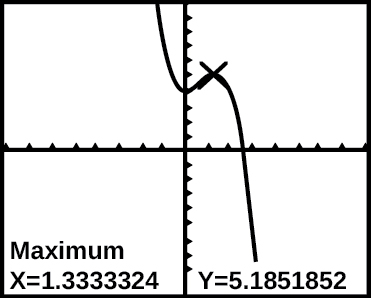
Based on the calculator screen shot, the point is which of the following?
A
Let Find a number such that the average rate of change of the function on the interval is
Let . Find the number such that the average rate of change of on the interval is
At the start of a trip, the odometer on a car read 21,395. At the end of the trip, 13.5 hours later, the odometer read 22,125. Assume the scale on the odometer is in miles. What is the average speed the car traveled during this trip?
A driver of a car stopped at a gas station to fill up his gas tank. He looked at his watch, and the time read exactly 3:40 p.m. At this time, he started pumping gas into the tank. At exactly 3:44, the tank was full and he noticed that he had pumped 10.7 gallons. What is the average rate of flow of the gasoline into the gas tank?
2.7 gallons per minute
Near the surface of the moon, the distance that an object falls is a function of time. It is given by where is in seconds and is in feet. If an object is dropped from a certain height, find the average velocity of the object from to
The graph in [link] illustrates the decay of a radioactive substance over days.
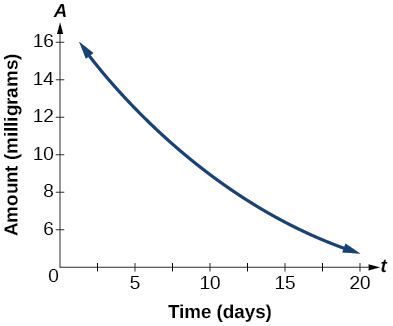
Use the graph to estimate the average decay rate from to
approximately –0.6 milligrams per day

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?