| << Chapter < Page | Chapter >> Page > |
Write an explicit formula for the term of the following geometric sequence.
The first term is 2. The common ratio can be found by dividing the second term by the first term.
The common ratio is 5. Substitute the common ratio and the first term of the sequence into the formula.
The graph of this sequence in [link] shows an exponential pattern.
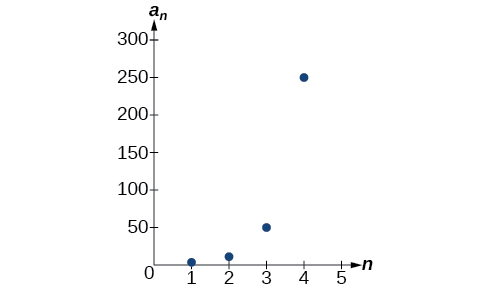
Write an explicit formula for the following geometric sequence.
In real-world scenarios involving arithmetic sequences, we may need to use an initial term of instead of In these problems, we can alter the explicit formula slightly by using the following formula:
In 2013, the number of students in a small school is 284. It is estimated that the student population will increase by 4% each year.
The situation can be modeled by a geometric sequence with an initial term of 284. The student population will be 104% of the prior year, so the common ratio is 1.04.
Let be the student population and be the number of years after 2013. Using the explicit formula for a geometric sequence we get
We can find the number of years since 2013 by subtracting.
We are looking for the population after 7 years. We can substitute 7 for to estimate the population in 2020.
The student population will be about 374 in 2020.
A business starts a new website. Initially the number of hits is 293 due to the curiosity factor. The business estimates the number of hits will increase by 2.6% per week.
Access these online resources for additional instruction and practice with geometric sequences.
| recursive formula for term of a geometric sequence | |
| explicit formula for term of a geometric sequence |

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?