1. Home
  2. College algebra
  3. Analytic geometry
  4. Rotation of axes

8.4 Rotation of axes  (Page 4/8)

<< Chapter < Page
  College algebra     Page 4 / 8
Chapter >> Page >

Rewrite the   13 x 2 − 6 3 x y + 7 y 2 = 16   in the   x ′ y ′   system without the   x ′ y ′   term.

x ′ 2 4 + y ′ 2 1 = 1

Got questions? Get instant answers now!

Graphing an equation that has no x′y′ Terms

Graph the following equation relative to the   x ′ y ′   system:

x 2 + 12 x y − 4 y 2 = 30

First, we find   cot ( 2 θ ) .

x 2 + 12 x y − 4 y 2 = 20 ⇒ A = 1 ,   B = 12 , and  C = −4
cot ( 2 θ ) = A − C B cot ( 2 θ ) = 1 − ( −4 ) 12 cot ( 2 θ ) = 5 12

Because   cot ( 2 θ ) = 5 12 , we can draw a reference triangle as in [link] .

cot ( 2 θ ) = 5 12 = adjacent opposite

Thus, the hypotenuse is

5 2 + 12 2 = h 2 25 + 144 = h 2 169 = h 2 h = 13

Next, we find   sin   θ   and   cos   θ .   We will use half-angle identities.

sin   θ = 1 − cos ( 2 θ ) 2 = 1 − 5 13 2 = 13 13 − 5 13 2 = 8 13 ⋅ 1 2 = 2 13 cos   θ = 1 + cos ( 2 θ ) 2 = 1 + 5 13 2 = 13 13 + 5 13 2 = 18 13 ⋅ 1 2 = 3 13

Now we find   x   and   y . 

x = x ′ cos   θ − y ′ sin   θ x = x ′ ( 3 13 ) − y ′ ( 2 13 ) x = 3 x ′ − 2 y ′ 13

and

y = x ′ sin   θ + y ′ cos   θ y = x ′ ( 2 13 ) + y ′ ( 3 13 ) y = 2 x ′ + 3 y ′ 13

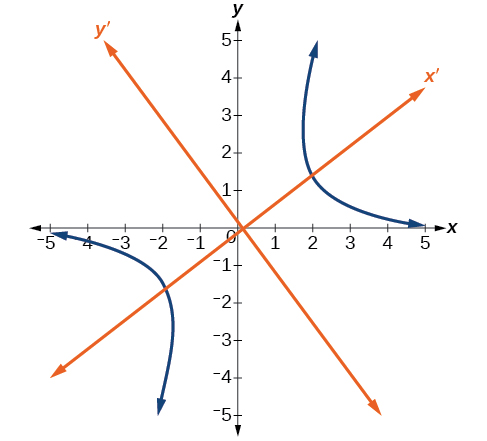
Now we substitute   x = 3 x ′ − 2 y ′ 13   and   y = 2 x ′ + 3 y ′ 13   into   x 2 + 12 x y − 4 y 2 = 30.

                                         ( 3 x ′ − 2 y ′ 13 ) 2 + 12 ( 3 x ′ − 2 y ′ 13 ) ( 2 x ′ + 3 y ′ 13 ) − 4 ( 2 x ′ + 3 y ′ 13 ) 2 = 30                                        ( 1 13 ) [ ( 3 x ′ − 2 y ′ ) 2 + 12 ( 3 x ′ − 2 y ′ ) ( 2 x ′ + 3 y ′ ) − 4 ( 2 x ′ + 3 y ′ ) 2 ] = 30   Factor . ( 1 13 ) [ 9 x ′ 2 − 12 x ′ y ′ + 4 y ′ 2 + 12 ( 6 x ′ 2 + 5 x ′ y ′ − 6 y ′ 2 ) − 4 ( 4 x ′ 2 + 12 x ′ y ′ + 9 y ′ 2 ) ] = 30 Multiply .    ( 1 13 ) [ 9 x ′ 2 − 12 x ′ y ′ + 4 y ′ 2 + 72 x ′ 2 + 60 x ′ y ′ − 72 y ′ 2 − 16 x ′ 2 − 48 x ′ y ′ − 36 y ′ 2 ] = 30 Distribute .                                                                                                      ( 1 13 ) [ 65 x ′ 2 − 104 y ′ 2 ] = 30 Combine like terms .                                                                                                             65 x ′ 2 − 104 y ′ 2 = 390 Multiply .                                                                                                                                     x ′ 2 6 − 4 y ′ 2 15 = 1   Divide by 390 .

[link] shows the graph of the hyperbola   x ′ 2 6 − 4 y ′ 2 15 = 1.       

Got questions? Get instant answers now!
Got questions? Get instant answers now!

Identifying conics without rotating axes

Now we have come full circle. How do we identify the type of conic described by an equation? What happens when the axes are rotated? Recall, the general form of a conic is

A x 2 + B x y + C y 2 + D x + E y + F = 0

If we apply the rotation formulas to this equation we get the form

A ′ x ′ 2 + B ′ x ′ y ′ + C ′ y ′ 2 + D ′ x ′ + E ′ y ′ + F ′ = 0

It may be shown that   B 2 − 4 A C = B ′ 2 − 4 A ′ C ′ .   The expression does not vary after rotation, so we call the expression invariant . The discriminant,   B 2 − 4 A C , is invariant and remains unchanged after rotation. Because the discriminant remains unchanged, observing the discriminant enables us to identify the conic section.

Using the discriminant to identify a conic

If the equation   A x 2 + B x y + C y 2 + D x + E y + F = 0   is transformed by rotating axes into the equation   A ′ x ′ 2 + B ′ x ′ y ′ + C ′ y ′ 2 + D ′ x ′ + E ′ y ′ + F ′ = 0 , then   B 2 − 4 A C = B ′ 2 − 4 A ′ C ′ .

The equation   A x 2 + B x y + C y 2 + D x + E y + F = 0   is an ellipse, a parabola, or a hyperbola, or a degenerate case of one of these.

If the discriminant,   B 2 − 4 A C , is

  • < 0 , the conic section is an ellipse
  • = 0 , the conic section is a parabola
  • > 0 , the conic section is a hyperbola

Identifying the conic without rotating axes

Identify the conic for each of the following without rotating axes.

  1. 5 x 2 + 2 3 x y + 2 y 2 − 5 = 0
  2. 5 x 2 + 2 3 x y + 12 y 2 − 5 = 0
  1. Let’s begin by determining   A , B , and   C .
    5 ︸ A x 2 + 2 3 ︸ B x y + 2 ︸ C y 2 − 5 = 0

    Now, we find the discriminant.

    B 2 − 4 A C = ( 2 3 ) 2 − 4 ( 5 ) ( 2 )                  = 4 ( 3 ) − 40                  = 12 − 40                  = − 28 < 0

    Therefore,   5 x 2 + 2 3 x y + 2 y 2 − 5 = 0   represents an ellipse.

  2. Again, let’s begin by determining   A , B , and   C .
    5 ︸ A x 2 + 2 3 ︸ B x y + 12 ︸ C y 2 − 5 = 0

    Now, we find the discriminant.

    B 2 − 4 A C = ( 2 3 ) 2 − 4 ( 5 ) ( 12 )                  = 4 ( 3 ) − 240                  = 12 − 240                  = − 228 < 0

    Therefore,   5 x 2 + 2 3 x y + 12 y 2 − 5 = 0   represents an ellipse.

Got questions? Get instant answers now!
Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>
Practice Key Terms 3

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, College algebra. OpenStax CNX. Feb 06, 2015 Download for free at https://legacy.cnx.org/content/col11759/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College algebra' conversation and receive update notifications?

Ask