| << Chapter < Page | Chapter >> Page > |
Graph the ellipse given by the equation Identify and label the center, vertices, co-vertices, and foci.
We must begin by rewriting the equation in standard form.
Group terms that contain the same variable, and move the constant to the opposite side of the equation.
Factor out the coefficients of the squared terms.
Complete the square twice. Remember to balance the equation by adding the same constants to each side.
Rewrite as perfect squares.
Divide both sides by the constant term to place the equation in standard form.
Now that the equation is in standard form, we can determine the position of the major axis. Because the major axis is parallel to the x -axis. Therefore, the equation is in the form where and It follows that:
Therefore, the coordinates of the foci are and
Next we plot and label the center, vertices, co-vertices, and foci, and draw a smooth curve to form the ellipse as shown in [link] .

Express the equation of the ellipse given in standard form. Identify the center, vertices, co-vertices, and foci of the ellipse.
center: vertices: and co-vertices: and foci: and
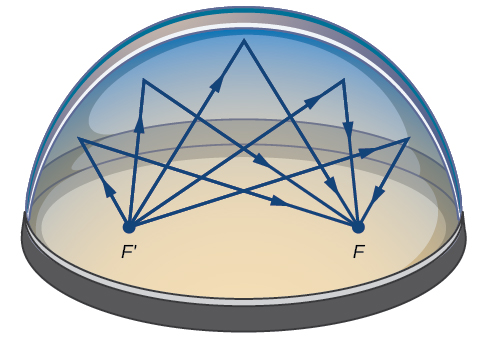
Many real-world situations can be represented by ellipses, including orbits of planets, satellites, moons and comets, and shapes of boat keels, rudders, and some airplane wings. A medical device called a lithotripter uses elliptical reflectors to break up kidney stones by generating sound waves. Some buildings, called whispering chambers, are designed with elliptical domes so that a person whispering at one focus can easily be heard by someone standing at the other focus. This occurs because of the acoustic properties of an ellipse. When a sound wave originates at one focus of a whispering chamber, the sound wave will be reflected off the elliptical dome and back to the other focus. See [link] . In the whisper chamber at the Museum of Science and Industry in Chicago, two people standing at the foci—about 43 feet apart—can hear each other whisper.
The Statuary Hall in the Capitol Building in Washington, D.C. is a whispering chamber. Its dimensions are 46 feet wide by 96 feet long as shown in [link] .
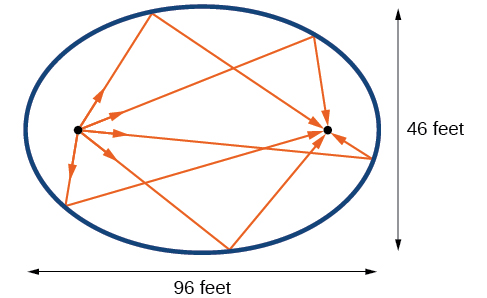
Therefore, the equation of the ellipse is
The points represent the foci. Thus, the distance between the senators is feet.

Notification Switch
Would you like to follow the 'College algebra' conversation and receive update notifications?