1. Home
  2. College algebra
  3. Analytic geometry
  4. The ellipse

8.1 The ellipse  (Page 4/16)

<< Chapter < Page
  College algebra     Page 4 / 16
Chapter >> Page >

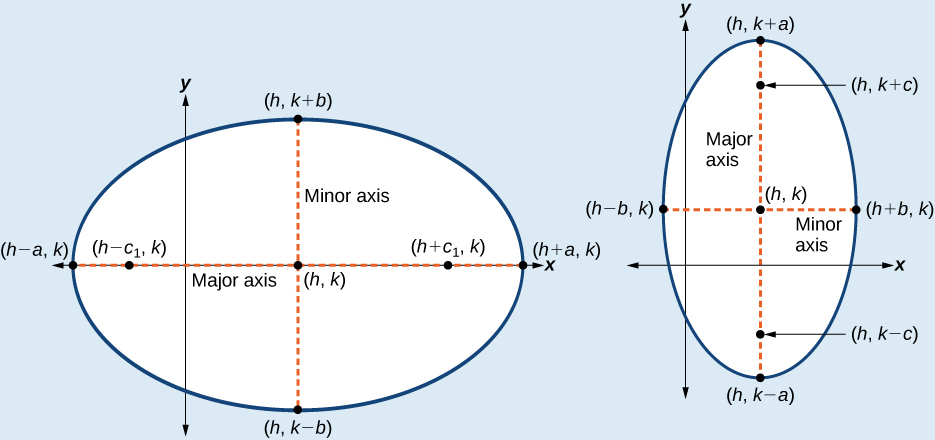
Standard forms of the equation of an ellipse with center ( h , k )

The standard form of the equation of an ellipse with center   ( h ,   k )   and major axis    parallel to the x -axis is

( x − h ) 2 a 2 + ( y − k ) 2 b 2 = 1

where

  • a > b
  • the length of the major axis is   2 a
  • the coordinates of the vertices are   ( h ± a , k )
  • the length of the minor axis is   2 b
  • the coordinates of the co-vertices are   ( h , k ± b )
  • the coordinates of the foci are   ( h ± c , k ) , where   c 2 = a 2 − b 2 .   See [link] a

The standard form of the equation of an ellipse with center   ( h , k )   and major axis parallel to the y -axis is

( x − h ) 2 b 2 + ( y − k ) 2 a 2 = 1

where

  • a > b
  • the length of the major axis is   2 a
  • the coordinates of the vertices are   ( h , k ± a )
  • the length of the minor axis is   2 b
  • the coordinates of the co-vertices are   ( h ± b , k )
  • the coordinates of the foci are   ( h , k ± c ) ,   where   c 2 = a 2 − b 2 .   See [link] b

Just as with ellipses centered at the origin, ellipses that are centered at a point   ( h , k )   have vertices, co-vertices, and foci that are related by the equation   c 2 = a 2 − b 2 .   We can use this relationship along with the midpoint and distance formulas to find the equation of the ellipse in standard form when the vertices and foci are given.

(a) Horizontal ellipse with center   ( h , k )   (b) Vertical ellipse with center   ( h , k )

Given the vertices and foci of an ellipse not centered at the origin, write its equation in standard form.

  1. Determine whether the major axis is parallel to the x - or y -axis.
    1. If the y -coordinates of the given vertices and foci are the same, then the major axis is parallel to the x -axis. Use the standard form   ( x − h ) 2 a 2 + ( y − k ) 2 b 2 = 1.
    2. If the x -coordinates of the given vertices and foci are the same, then the major axis is parallel to the y -axis. Use the standard form   ( x − h ) 2 b 2 + ( y − k ) 2 a 2 = 1.
  2. Identify the center of the ellipse   ( h , k )   using the midpoint formula and the given coordinates for the vertices.
  3. Find   a 2   by solving for the length of the major axis,   2 a , which is the distance between the given vertices.
  4. Find   c 2   using   h   and   k , found in Step 2, along with the given coordinates for the foci.
  5. Solve for   b 2   using the equation   c 2 = a 2 − b 2 .
  6. Substitute the values for   h , k , a 2 , and   b 2   into the standard form of the equation determined in Step 1.

Writing the equation of an ellipse centered at a point other than the origin

What is the standard form equation of the ellipse that has vertices   ( −2 , −8 )   and   ( −2 , 2 )

and foci   ( −2 , −7 )   and   ( −2 , 1 ) ?

The x -coordinates of the vertices and foci are the same, so the major axis is parallel to the y -axis. Thus, the equation of the ellipse will have the form

( x − h ) 2 b 2 + ( y − k ) 2 a 2 = 1

First, we identify the center,   ( h , k ) .   The center is halfway between the vertices,   ( − 2, − 8 )   and   ( − 2 , 2 ) .   Applying the midpoint formula, we have:

( h , k ) = ( −2 + ( −2 ) 2 , −8 + 2 2 )           = ( −2 , −3 )

Next, we find   a 2 .   The length of the major axis,   2 a , is bounded by the vertices. We solve for   a   by finding the distance between the y -coordinates of the vertices.

                                2 a = 2 − ( −8 ) 2 a = 10 a = 5

So   a 2 = 25.

Now we find   c 2 .   The foci are given by   ( h , k ± c ) .   So,   ( h , k − c ) = ( −2 , −7 )   and   ( h , k + c ) = ( −2 , 1 ) .   We substitute   k = −3   using either of these points to solve for   c .

        k + c = 1 −3 + c = 1                             c = 4

So   c 2 = 16.

Next, we solve for   b 2   using the equation   c 2 = a 2 − b 2 .

                            c 2 = a 2 − b 2                             16 = 25 − b 2 b 2 = 9

Finally, we substitute the values found for   h , k , a 2 , and   b 2   into the standard form equation for an ellipse:

  ( x + 2 ) 2 9 + ( y + 3 ) 2 25 = 1
Got questions? Get instant answers now!
Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>
Practice Key Terms 7

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, College algebra. OpenStax CNX. Feb 06, 2015 Download for free at https://legacy.cnx.org/content/col11759/1.3
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'College algebra' conversation and receive update notifications?

Ask