7.2 Systems of linear equations: three variables  (Page 2/8)

We will check each equation by substituting in the values of the ordered triple for $x,y,$ and $z.$

$\begin{array}{ccccc}\begin{array}{r}\hfill x+y+z=2\\ \hfill (3)+(\mathrm{-2})+(1)=2\\ \hfill \text{True}\end{array}& & \begin{array}{r}\hfill 6x\mathrm{-4}y+5z=31\\ \hfill 6(3)\mathrm{-4}(\mathrm{-2})+5(1)=31\\ \hfill 18+8+5=31\\ \hfill \text{True}\end{array}& & \begin{array}{r}\hfill 5x+2y+2z=13\\ \hfill 5(3)+2(\mathrm{-2})+2(1)=13\\ \hfill 15\mathrm{-4}+2=13\\ \hfill \text{True}\end{array}\end{array}$

The ordered triple $\left(3,\mathrm{-2},1\right)$ is indeed a solution to the system.

There will always be several choices as to where to begin, but the most obvious first step here is to eliminate $x$ by adding equations (1) and (2).

The second step is multiplying equation (1) by $\mathrm{-2}$ and adding the result to equation (3). These two steps will eliminate the variable $x.$

In equations (4) and (5), we have created a new two-by-two system. We can solve for $z$ by adding the two equations.

Choosing one equation from each new system, we obtain the upper triangular form:

Next, we back-substitute $z=2$ into equation (4) and solve for $y.$

Finally, we can back-substitute $z=2$ and $y=\mathrm{-1}$ into equation (1). This will yield the solution for $x.$

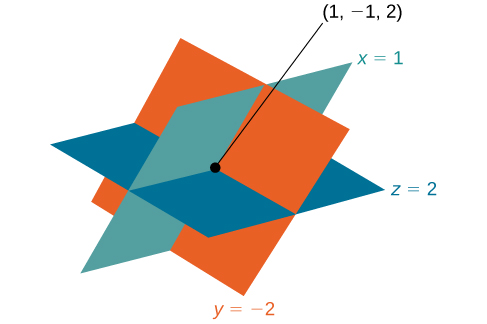
The solution is the ordered triple $\left(1,\mathrm{-1},2\right).$ See [link] .