| << Chapter < Page | Chapter >> Page > |
Suppose we want to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and in turn, the average daily temperature depends on the particular day of the year. Notice how we have just defined two relationships: The cost depends on the temperature, and the temperature depends on the day.
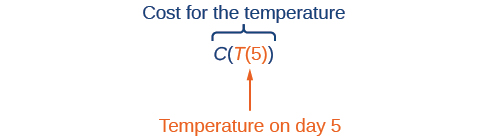
Using descriptive variables, we can notate these two functions. The function gives the cost of heating a house for a given average daily temperature in degrees Celsius. The function gives the average daily temperature on day of the year. For any given day, means that the cost depends on the temperature, which in turns depends on the day of the year. Thus, we can evaluate the cost function at the temperature For example, we could evaluate to determine the average daily temperature on the 5th day of the year. Then, we could evaluate the cost function at that temperature. We would write
By combining these two relationships into one function, we have performed function composition, which is the focus of this section.
Function composition is only one way to combine existing functions. Another way is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication and division. We do this by performing the operations with the function outputs, defining the result as the output of our new function.
Suppose we need to add two columns of numbers that represent a husband and wife’s separate annual incomes over a period of years, with the result being their total household income. We want to do this for every year, adding only that year’s incomes and then collecting all the data in a new column. If is the wife’s income and is the husband’s income in year and we want to represent the total income, then we can define a new function.
If this holds true for every year, then we can focus on the relation between the functions without reference to a year and write
Just as for this sum of two functions, we can define difference, product, and ratio functions for any pair of functions that have the same kinds of inputs (not necessarily numbers) and also the same kinds of outputs (which do have to be numbers so that the usual operations of algebra can apply to them, and which also must have the same units or no units when we add and subtract). In this way, we can think of adding, subtracting, multiplying, and dividing functions.
For two functions and with real number outputs, we define new functions and by the relations

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?