1. Home
  2. Algebra and trigonometry
  3. Equations and inequalities
  4. The rectangular coordinate

2.1 The rectangular coordinate systems and graphs  (Page 4/21)

<< Chapter < Page
  Algebra and trigonometry     Page 4 / 21
Chapter >> Page >
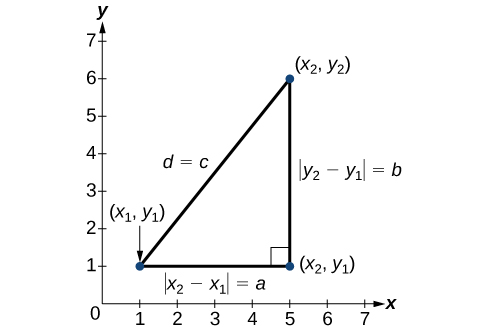
This is an image of a triangle on an x, y coordinate plane. The x and y axes range from 0 to 7. The points (x sub 1, y sub 1); (x sub 2, y sub 1); and (x sub 2, y sub 2) are labeled and connected to form a triangle. Along the base of the triangle, the following equation is displayed: the absolute value of x sub 2 minus x sub 1 equals a. The hypotenuse of the triangle is labeled: d = c. The remaining side is labeled: the absolute value of y sub 2 minus y sub 1 equals b.

The relationship of sides   | x 2 − x 1 |   and   | y 2 − y 1 |   to side d is the same as that of sides a and b to side c. We use the absolute value symbol to indicate that the length is a positive number because the absolute value of any number is positive. (For example,   | −3 | = 3.   ) The symbols   | x 2 − x 1 |   and   | y 2 − y 1 |   indicate that the lengths of the sides of the triangle are positive. To find the length c , take the square root of both sides of the Pythagorean Theorem.

c 2 = a 2 + b 2 → c = a 2 + b 2

It follows that the distance formula is given as

d 2 = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 → d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2

We do not have to use the absolute value symbols in this definition because any number squared is positive.

The distance formula

Given endpoints   ( x 1 , y 1 )   and   ( x 2 , y 2 ) , the distance between two points is given by

d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2

Finding the distance between two points

Find the distance between the points   ( −3 , −1 )   and   ( 2 , 3 ) .

Let us first look at the graph of the two points. Connect the points to form a right triangle as in [link] .

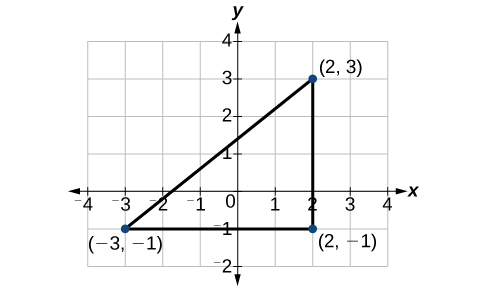
This is an image of a triangle on an x, y coordinate plane. The x-axis ranges from negative 4 to 4. The y-axis ranges from negative 2 to 4. The points (-3, -1); (2, -1); and (2, 3) are plotted and labeled on the graph. The points are connected to form a triangle

Then, calculate the length of d using the distance formula.

d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 d = ( 2 − ( −3 ) ) 2 + ( 3 − ( −1 ) ) 2 = ( 5 ) 2 + ( 4 ) 2 = 25 + 16 = 41
Got questions? Get instant answers now!
Got questions? Get instant answers now!

Find the distance between two points:   ( 1 , 4 )   and   ( 11 , 9 ) .

125 = 5 5

Got questions? Get instant answers now!

Finding the distance between two locations

Let’s return to the situation introduced at the beginning of this section.

Tracie set out from Elmhurst, IL, to go to Franklin Park. On the way, she made a few stops to do errands. Each stop is indicated by a red dot in [link] . Find the total distance that Tracie traveled. Compare this with the distance between her starting and final positions.

The first thing we should do is identify ordered pairs to describe each position. If we set the starting position at the origin, we can identify each of the other points by counting units east (right) and north (up) on the grid. For example, the first stop is 1 block east and 1 block north, so it is at   ( 1 , 1 ) .   The next stop is 5 blocks to the east, so it is at   ( 5 , 1 ) .   After that, she traveled 3 blocks east and 2 blocks north to   ( 8 , 3 ) .   Lastly, she traveled 4 blocks north to   ( 8 , 7 ) .   We can label these points on the grid as in [link] .

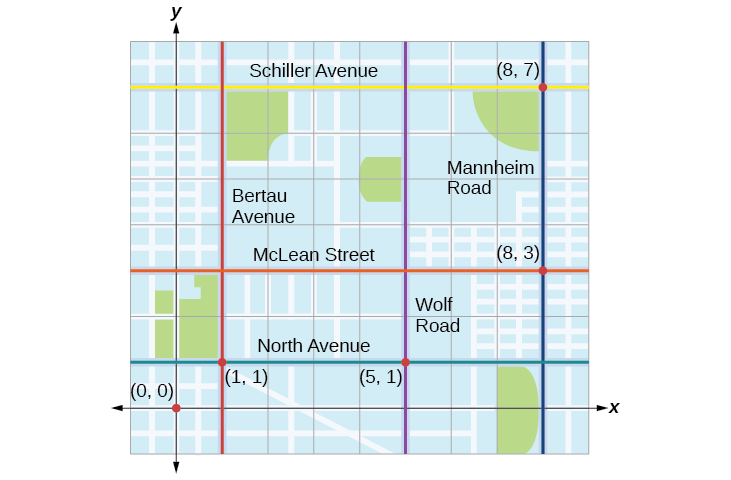
This is an image of a road map of a city. The point (1, 1) is on North Avenue and Bertau Avenue. The point (5, 1) is on North Avenue and Wolf Road. The point (8, 3) is on Mannheim Road and McLean Street. The point (8, 7) is on Mannheim Road and Schiller Avenue.

Next, we can calculate the distance. Note that each grid unit represents 1,000 feet.

  • From her starting location to her first stop at   ( 1 , 1 ) , Tracie might have driven north 1,000 feet and then east 1,000 feet, or vice versa. Either way, she drove 2,000 feet to her first stop.
  • Her second stop is at   ( 5 , 1 ) .   So from   ( 1 , 1 )   to   ( 5 , 1 ) , Tracie drove east 4,000 feet.
  • Her third stop is at   ( 8 , 3 ) .   There are a number of routes from   ( 5 , 1 )   to   ( 8 , 3 ) .   Whatever route Tracie decided to use, the distance is the same, as there are no angular streets between the two points. Let’s say she drove east 3,000 feet and then north 2,000 feet for a total of 5,000 feet.
  • Tracie’s final stop is at   ( 8 , 7 ) .   This is a straight drive north from   ( 8 , 3 )   for a total of 4,000 feet.

Next, we will add the distances listed in [link] .

From/To Number of Feet Driven
( 0 , 0 )   to   ( 1 , 1 ) 2,000
( 1 , 1 )   to ( 5 , 1 )   4,000
( 5 , 1 )   to   ( 8 , 3 ) 5,000
( 8 , 3 )   to   ( 8 , 7 ) 4,000
Total 15,000

The total distance Tracie drove is 15,000 feet, or 2.84 miles. This is not, however, the actual distance between her starting and ending positions. To find this distance, we can use the distance formula between the points   ( 0 , 0 )   and   ( 8 , 7 ) .

d = ( 8 − 0 ) 2 + ( 7 − 0 ) 2 = 64 + 49 = 113 = 10.63  units

At 1,000 feet per grid unit, the distance between Elmhurst, IL, to Franklin Park is 10,630.14 feet, or 2.01 miles. The distance formula results in a shorter calculation because it is based on the hypotenuse of a right triangle, a straight diagonal from the origin to the point   ( 8 , 7 ) .   Perhaps you have heard the saying “as the crow flies,” which means the shortest distance between two points because a crow can fly in a straight line even though a person on the ground has to travel a longer distance on existing roadways.

Got questions? Get instant answers now!
<< Chapter < Page Page > Chapter >>
Practice Key Terms 15

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

Get it on Google Play Download on the App Store Now




Source:  OpenStax, Algebra and trigonometry. OpenStax CNX. Nov 14, 2016 Download for free at https://legacy.cnx.org/content/col11758/1.6
Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?

Ask